Предмет: Геометрия,
автор: УченикЛадушка7
Докажите что бесектриса угла треугольника и бесектриса внешнего угла,проведенный из одной вершины,перпендикулярны
Ответы
Автор ответа:
2
угол при вершине треугольника пусть равен x. тогда углы, отсекаемые биссектрисой этого угла, равны x/2. внешний угол при той же вершине равен 180-x. значит углы, отсекаемые биссектрисой этого угла, равны 90-x/2. угол между двумя биссектрисами равен x/2+90-x/2=90, чтд.
Автор ответа:
2
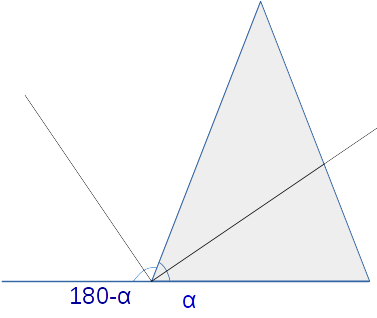
Насколько я помню сумма внешнего угла и внутреннего угла треугольника 180°. Т.е. обозначив α внутренний угол, получим, что внешний равен 180-α
Биссектриса внутреннего угла делит его пополам получаем α/2. Половинка внешнего угла (180-α)/2. Угол между биссектрисами равен сумме этих половинок: α/2+(180-α)/2=α/2+180/2-α/2=180/2=90
QED
Биссектриса внутреннего угла делит его пополам получаем α/2. Половинка внешнего угла (180-α)/2. Угол между биссектрисами равен сумме этих половинок: α/2+(180-α)/2=α/2+180/2-α/2=180/2=90
QED
Приложения:
Exponena:
Вот почему я не видел, что правильный ответ уже дан. Я бы и не начинал.
???
Похожие вопросы
Предмет: Русский язык,
автор: 1997шахзод
Предмет: Русский язык,
автор: серутиус
Предмет: Русский язык,
автор: Аноним
Предмет: Алгебра,
автор: dkspfdskf
Предмет: История,
автор: picnic212121