Предмет: Алгебра,
автор: chopay
Решите пожалуйста по подробнее
Приложения:
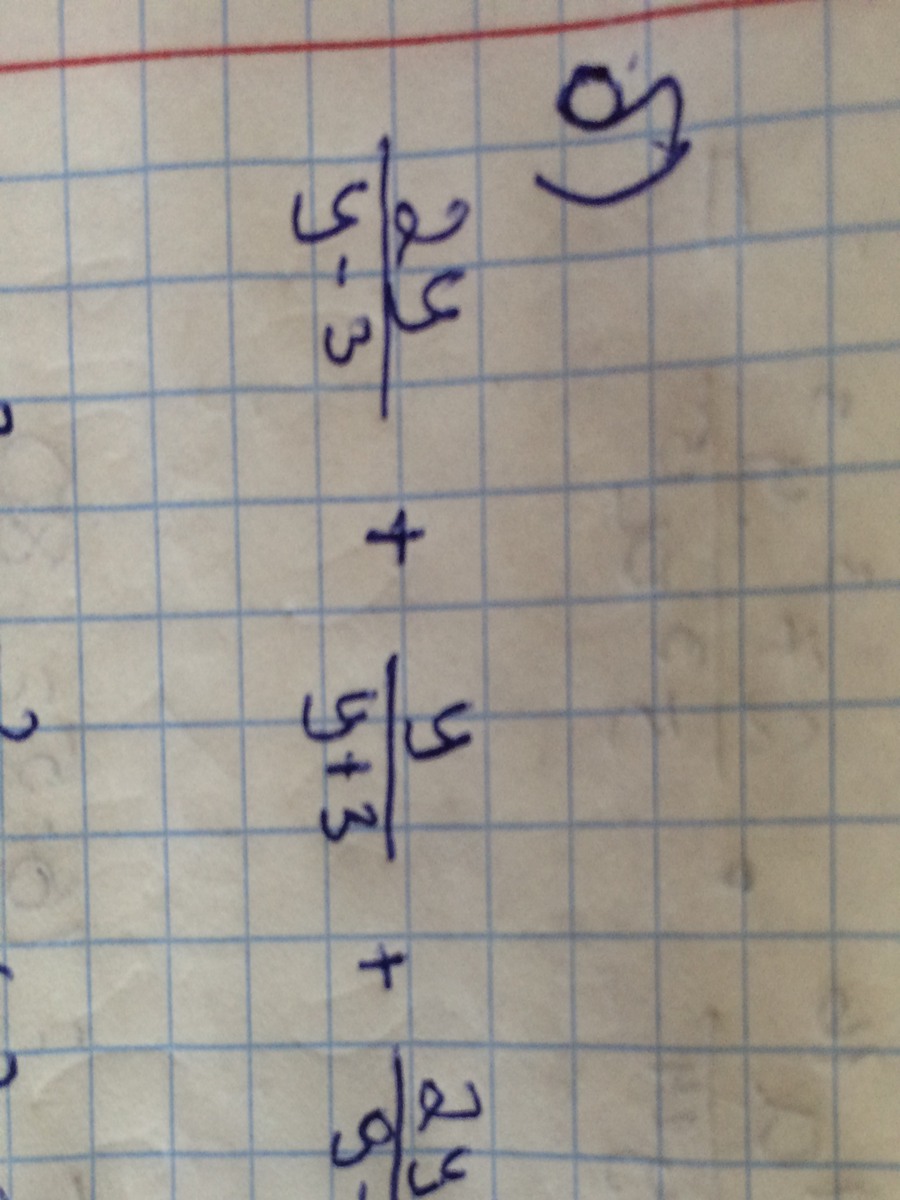
chopay:
в третьей дроби знаменатель 9-y2
Ответы
Автор ответа:
0
Решение:
2у/(у-3)+у/(у+3) Приведём данное выражение к обшему знаменателю: (у-3)*(у+3)
Кстати знаменатель можно свернуть: (у²-9) (достаточно вспомнить формулу:
(а²-b²)=(a-b)*(a+b)
Итак:
(2у+у)/(у²-9)=3у/(у²-9)
Ответ: 3у/(у²-9)
2у/(у-3)+у/(у+3) Приведём данное выражение к обшему знаменателю: (у-3)*(у+3)
Кстати знаменатель можно свернуть: (у²-9) (достаточно вспомнить формулу:
(а²-b²)=(a-b)*(a+b)
Итак:
(2у+у)/(у²-9)=3у/(у²-9)
Ответ: 3у/(у²-9)
/-это деление?
Да это деление!
Автор ответа:
0
Считаю, что решено неправильно.
Третью дробь не заметили
А решение правильное
У меня не видно третье слагаемое. Если так, то может и верно, не знаю
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: арина12324
Предмет: Другие предметы,
автор: norvardmanukya
Предмет: Английский язык,
автор: bondarenkoneki
Предмет: Обществознание,
автор: wwwm0leundlip03