Предмет: Алгебра,
автор: uh19
интеграл....................................
Приложения:
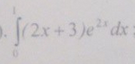
uh19:
Спасибо Вам большое. Никого не хочу обидеть отмечая "лучший", поэтому в одном задании отмечу DimaPuchkov, в другом Manyny06.
Ответы
Автор ответа:
1
Интегрируем по частям



Автор ответа:
1
решение смотри на фотографии
Приложения:

Похожие вопросы
Предмет: Українська мова,
автор: milasenkiy
Предмет: Русский язык,
автор: ksyha1234
Предмет: Русский язык,
автор: 1234567890870
Предмет: Русский язык,
автор: gauteeer
Предмет: Химия,
автор: eldargambit