Предмет: Алгебра,
автор: uh19
интеграл...................................
Приложения:
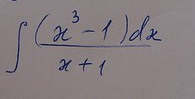
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Русский язык,
автор: мимиСержик1
Предмет: Русский язык,
автор: kabilet777
Предмет: Русский язык,
автор: maximmanastyrl
Предмет: Английский язык,
автор: nargiz851