Предмет: Алгебра,
автор: uh19
интеграл..............................................
Приложения:
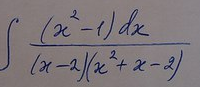
Ответы
Автор ответа:
2
Автор ответа:
1
Решение в файле................
Приложения:


Похожие вопросы
Предмет: Русский язык,
автор: maximmanastyrl
Предмет: Русский язык,
автор: Oksanochka101
Предмет: Русский язык,
автор: ofeliya1987
Предмет: Математика,
автор: nick9016
Предмет: Математика,
автор: muzalina2007