Предмет: Алгебра,
автор: Arinis
Решите пожалуйста одно неравенство! Есть фотография
Приложения:
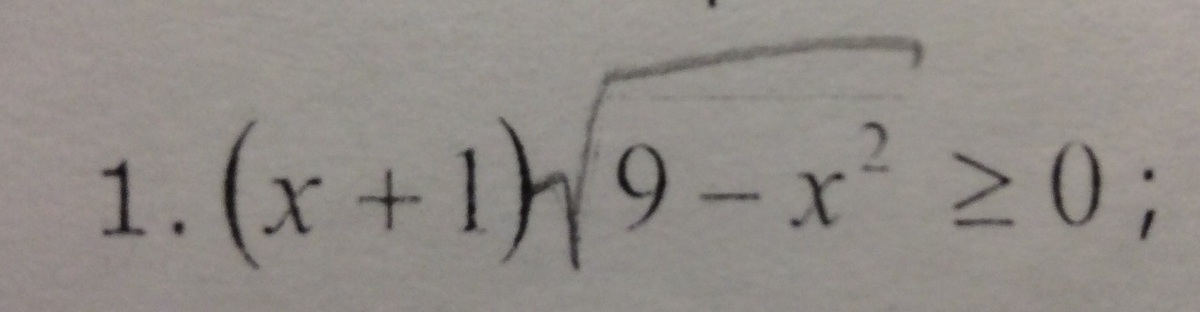
Ответы
Автор ответа:
1
Выражение под корнем всегда больше или равно нулю

ОДЗ:
- + -
-------*-------*-------->x
-3 3

В итоге получим
но при неравенство также выполняется
неравенство также выполняется
Ответ:![{-3}; \ [-1;3] {-3}; \ [-1;3]](https://tex.z-dn.net/?f=%7B-3%7D%3B+%5C+%5B-1%3B3%5D)
ОДЗ:
- + -
-------*-------*-------->x
-3 3
В итоге получим
но при
Ответ:
Похожие вопросы
Предмет: Русский язык,
автор: 467536886
Предмет: Английский язык,
автор: Katrin0308
Предмет: Английский язык,
автор: garikonik
Предмет: Информатика,
автор: aniraeee