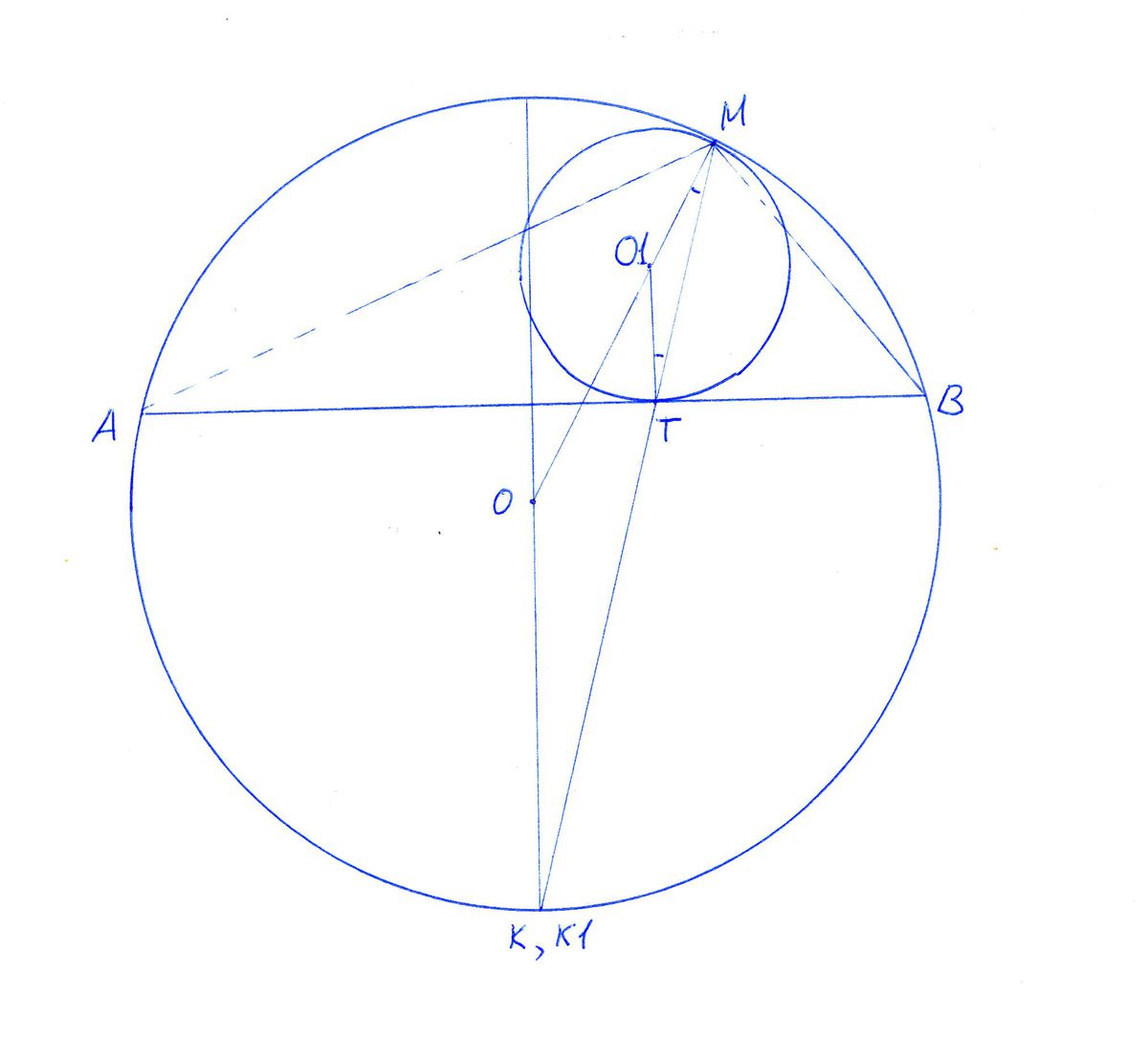
Две окружности касаются внутренним образом в точке M. Пусть AB — хорда большей окружности, касающаяся меньшей окружности в точке T. Известно, что AT=7, BT=4. Найдите отношение AM/BM
Ответы
Пусть KO - диаметр большей окружности, перпендикулярный AB. Точка K лежит на большей окружности. Этот диаметр (проходящий через O перпендикулярно AB) делит пополам и хорду AB, и обе дуги AB - большую и малую.
Ясно, что KO II O1T; так как O1T тоже перпендикулярно AB.
Пусть прямая MT пересекает большую окружность в точке K1.
На чертеже эти точки K и K1 изображены, как одна - но именно это и есть предмет доказательства. Я буду доказывать, что точка K1 - середина большой дуги AB, то есть совпадает с точкой K.
Важно не забывать, что точка касания M лежит на линии центров OO1.
Треугольники OK1M и O1TM оба равнобедренные, и имеют общий угол OMT, следовательно, они подобны (из того, что есть один общий угол "при основании" у двух равнобедренных треугольников, следует, что все соответственные углы этих треугольников равны).
Поэтому OK1 II O1T; (легко увидеть признак параллельности равенство углов при секущей OM :) )
Ну, дальше - обычное заклинание "через точку O можно провести только одну прямую параллельную O1T". То есть точки K и K1 совпадают.
Это означает, что прямая MT, будучи продолжена за точку T, делит дугу AKB пополам (я напомню, что KO - диаметр, перпендикулярный хорде AB, поэтому точка K делит дугу AKB пополам. ).
Углы AMK и BMK - вписанные и опираются на равные дуги, поэтому они равны. Следовательно MT - биссектриса угла AMB;
AM/MB = AT/BT = 7/4;