Предмет: Алгебра,
автор: alyonaparshina
Найти tg a, если 3cos a + 2sin a / sin a + 2cos a = 1,6
Приложения:
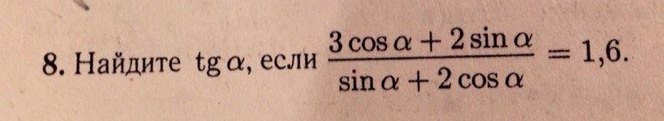
Ответы
Автор ответа:
4
Преобразуем левую часть.
Т.е получаем
проводим замену переменной, чтобы не таскаться с тангенсом (хотя и не обязательно)
alyonaparshina:
Огромное спасибо!
Похожие вопросы
Предмет: Русский язык,
автор: Hiera
Предмет: Английский язык,
автор: Даша26052004
Предмет: Английский язык,
автор: Орошник
Предмет: Математика,
автор: 1010010
Предмет: Физика,
автор: masha13032000