Предмет: Алгебра,
автор: zaznaika96
помогите пожалуйста с интегралом 
Ответы
Автор ответа:
1
Смотреть во вложении
Приложения:
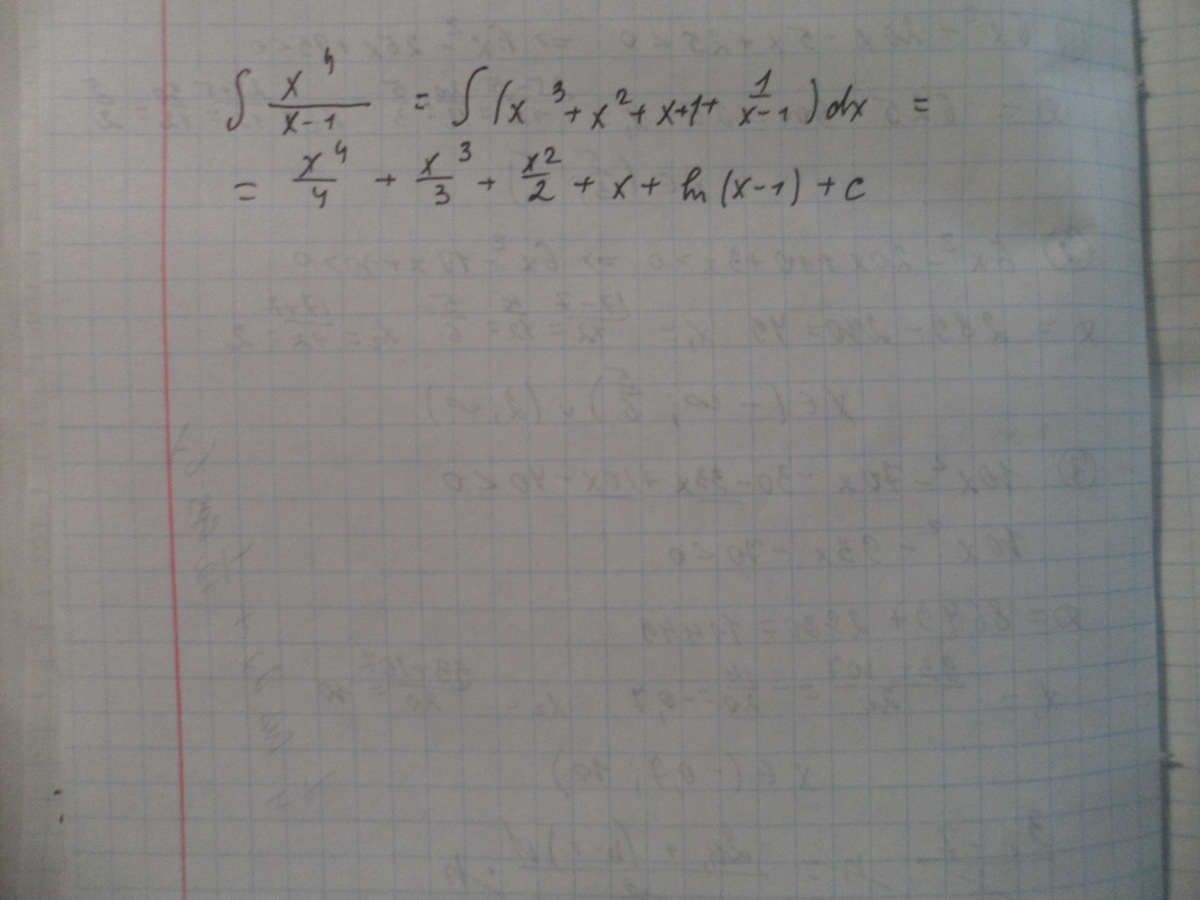
Автор ответа:
1
Преобразуем числитель
х⁴=х⁴-1+1=(х⁴-1)=1=(х²-1)(х²+1)+1=(х-1)(х+1)(х²+1)+1

Под знаком логарифма (х-1) надо написать по модулю.
х⁴=х⁴-1+1=(х⁴-1)=1=(х²-1)(х²+1)+1=(х-1)(х+1)(х²+1)+1
Под знаком логарифма (х-1) надо написать по модулю.
Похожие вопросы
Предмет: Окружающий мир,
автор: КайфДрайф
Предмет: Русский язык,
автор: JannaDipper
Предмет: Беларуская мова,
автор: место33
Предмет: Қазақ тiлi,
автор: katsumy
Предмет: Математика,
автор: angel1angel