Предмет: Алгебра,
автор: alyakurganovaСаня
Ребят решить надо сегодня
помогите
под 15 номером а) и б)
Приложения:

Ответы
Автор ответа:
1
Использована формула косинуса двойного угла, определение тангенса
Приложения:
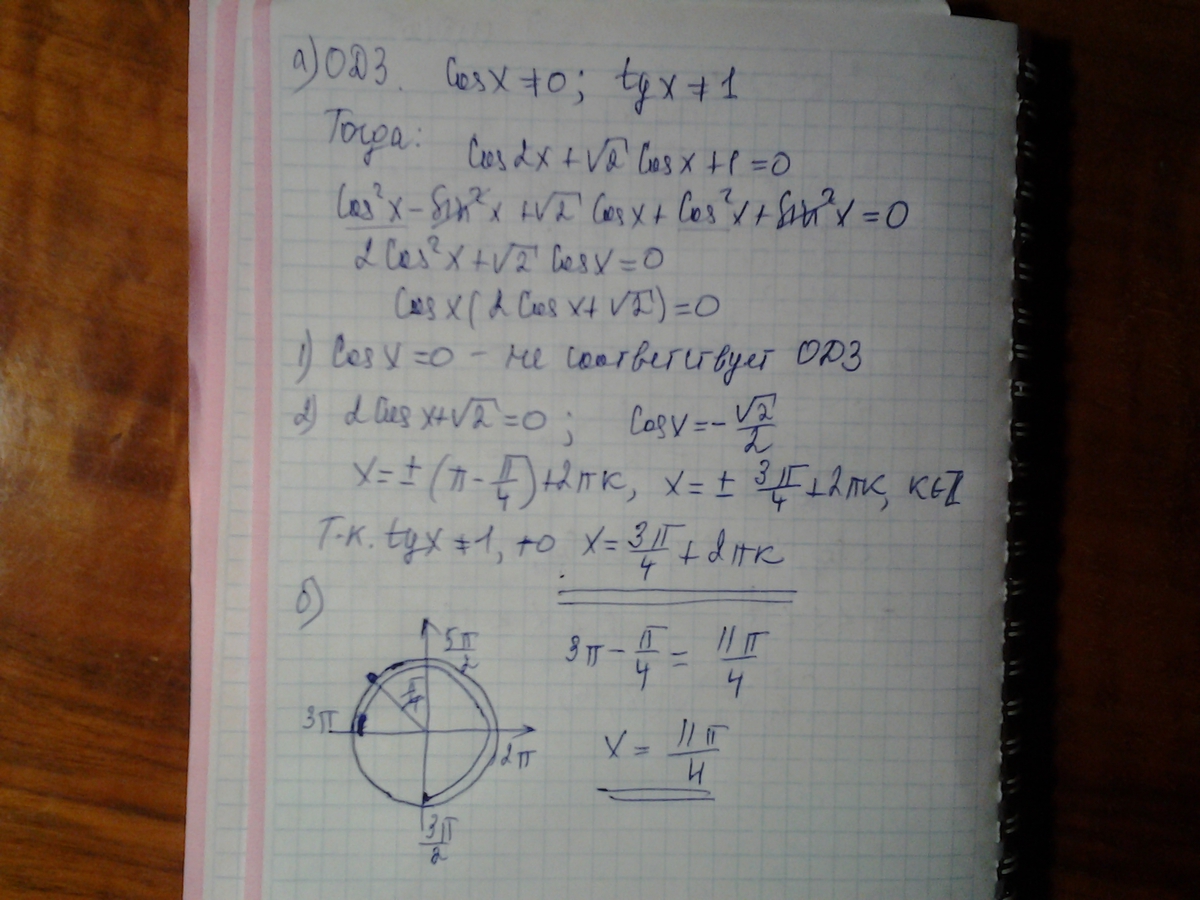
Автор ответа:
1
n,k,m ∈ Z
Похожие вопросы
Предмет: Русский язык,
автор: akonya131
Предмет: Русский язык,
автор: San4ic
Предмет: Английский язык,
автор: Mavpohka
Предмет: История,
автор: yuitaigga
Предмет: Алгебра,
автор: nn8255241