Предмет: Алгебра,
автор: Аноним
СРОЧНО! Решите неравенство 2x+1/x+3≦1 и запишите количество целых решений
Напишите подробно как решать, мне важно именно объяснение
Ответы
Автор ответа:
1
(2x+1)/(x+3) ≤ 1
(2x+1)/(x+3) - 1 ≤ 0
Рассмотрим функцию
f(x) = (2x+1)/(x+3) - 1
Область определения функции
x+3≠0
x≠-3
D(f) = (-∞;-3)U(-3;+∞)
Нули функции
f(x)=0
(2x+1)/(x+3) = 1 |*(x+3)
2x+1 = x+3
2x - x = 3 - 1
x = 2
__+__(-3)__-__[2]__+__>
х ∈ (-3;2]
Целые числа: -2; -1; 0; 1; 2
Количество целых чисел: 5
(2x+1)/(x+3) - 1 ≤ 0
Рассмотрим функцию
f(x) = (2x+1)/(x+3) - 1
Область определения функции
x+3≠0
x≠-3
D(f) = (-∞;-3)U(-3;+∞)
Нули функции
f(x)=0
(2x+1)/(x+3) = 1 |*(x+3)
2x+1 = x+3
2x - x = 3 - 1
x = 2
__+__(-3)__-__[2]__+__>
х ∈ (-3;2]
Целые числа: -2; -1; 0; 1; 2
Количество целых чисел: 5
Автор ответа:
1
Решение смотри в приложении
Приложения:
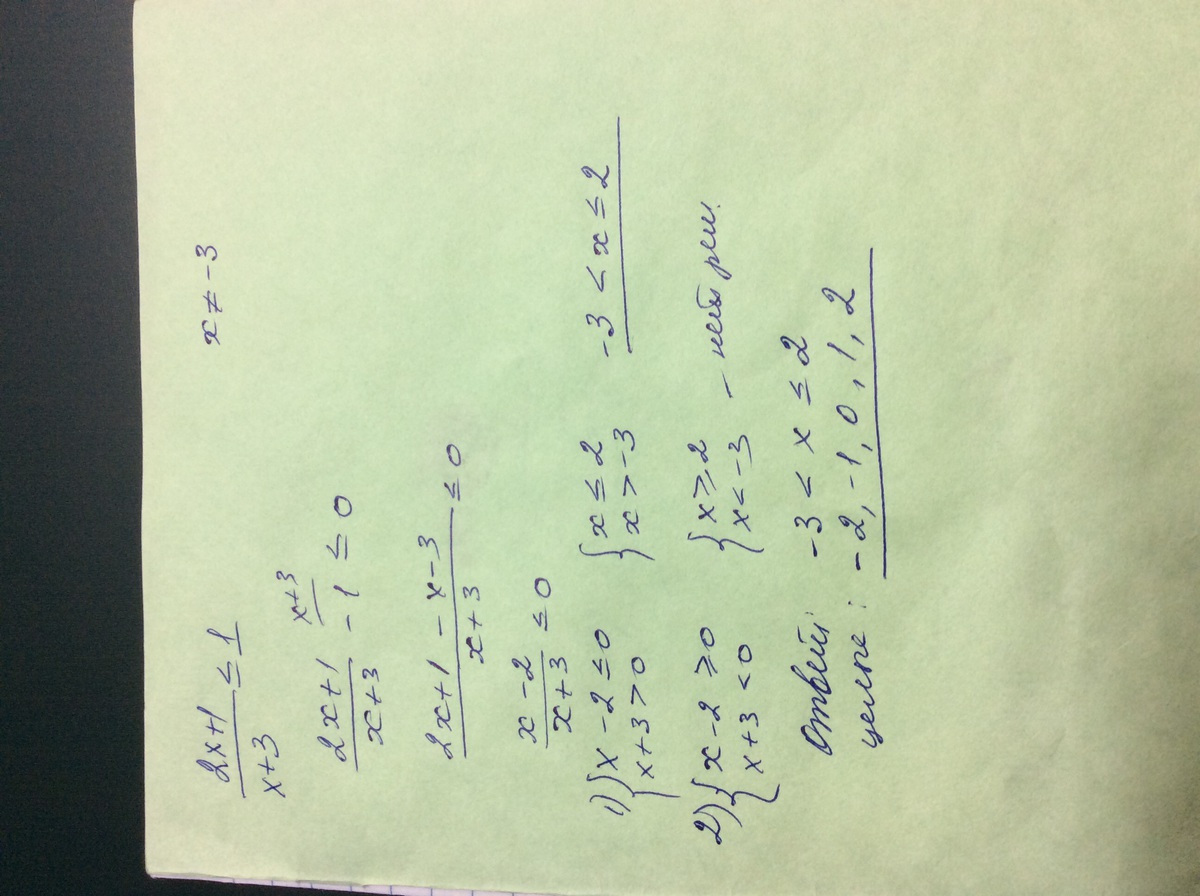
Похожие вопросы
Предмет: Русский язык,
автор: maxhatsune1337
Предмет: Русский язык,
автор: angelinaignaty1
Предмет: Русский язык,
автор: natilona
Предмет: Математика,
автор: nikitalapa
Предмет: Физика,
автор: demidondanil