Предмет: Алгебра,
автор: Himerra
запишите в виде степени с рациональным показателем( там квадратный корень в степени 4, и в степени 3)
Приложения:
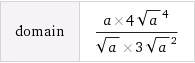
Ответы
Автор ответа:
2
Автор ответа:
0
Квадратный корень в степени 4 или корень 4-й степени.? Ладно рассмотрим оба варианта


Тут можно было быстрее (сократить сразу на a, но результат не изменится).
Если условие понимать иначе, то так
![\frac{a*\sqrt[4]{a^4} }{ \sqrt{a}* \sqrt[3]{a^2} }= \frac{a*a^{4/4} }{ a^{1/2}* a^{2/3} } =\frac{a^{2} }{ a^{(1/2+2/3)} }=\frac{a^{2} }{ a^{(3/6+4/6)} }=\frac{a^{2} }{ a^{7/6} }=a^{2} * a^{-7/6}= \frac{a*\sqrt[4]{a^4} }{ \sqrt{a}* \sqrt[3]{a^2} }= \frac{a*a^{4/4} }{ a^{1/2}* a^{2/3} } =\frac{a^{2} }{ a^{(1/2+2/3)} }=\frac{a^{2} }{ a^{(3/6+4/6)} }=\frac{a^{2} }{ a^{7/6} }=a^{2} * a^{-7/6}=](https://tex.z-dn.net/?f=%5Cfrac%7Ba%2A%5Csqrt%5B4%5D%7Ba%5E4%7D+%7D%7B+%5Csqrt%7Ba%7D%2A+%5Csqrt%5B3%5D%7Ba%5E2%7D+%7D%3D+%5Cfrac%7Ba%2Aa%5E%7B4%2F4%7D+%7D%7B+a%5E%7B1%2F2%7D%2A+a%5E%7B2%2F3%7D+%7D+%3D%5Cfrac%7Ba%5E%7B2%7D+%7D%7B+a%5E%7B%281%2F2%2B2%2F3%29%7D+%7D%3D%5Cfrac%7Ba%5E%7B2%7D+%7D%7B+a%5E%7B%283%2F6%2B4%2F6%29%7D+%7D%3D%5Cfrac%7Ba%5E%7B2%7D+%7D%7B+a%5E%7B7%2F6%7D+%7D%3Da%5E%7B2%7D+%2A+a%5E%7B-7%2F6%7D%3D)

Тут можно было быстрее (сократить сразу на a, но результат не изменится).
Если условие понимать иначе, то так
Похожие вопросы
Предмет: Русский язык,
автор: lizzza77
Предмет: Немецкий язык,
автор: larinastuscha1
Предмет: Английский язык,
автор: Нихан1111
Предмет: Математика,
автор: Minella