Предмет: Математика,
автор: liska16
Помогите пожалуйста решить хоть что-то))
Приложения:
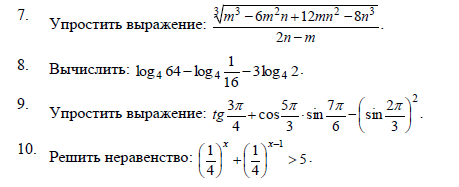
Ответы
Автор ответа:
1
7. = ∛(m-2n)³ = m-2n = -1
2n-m -(m-2n)
8. = log₄ 4³ - log₄ 4⁻² - 3log₄ 4¹/² =3-(-2)-3*(1/2)=3+2-1.5=3.5
9.
tg(3π/4)=tg(4π/4 - π/4) = -tg(π/4)=-1
cos(5π/3)=cos(6π/3 - π/3) =cos(π/3)=1/2
sin(7π/6)=sin(6π/6 + π/6)=-sin(π/6)=-1/2
sin(2π/3)=sin(3π/3 - π/3) = sin (π/3)=√3/2
-1+(1/2)*(-1/2)-(√3/2)²=-1-(1/4)-(3/4)=-1-1=-2
10.
(1/4)^x + (1/4)^(x-1)>5
(1/4)^x (1+(1/4)⁻¹)>5
(1/4)^x (1+4)>5
(1/4)^x * 5>5
(1/4)^x>1
(1/4)^x >(1/4)⁰
x<0
2n-m -(m-2n)
8. = log₄ 4³ - log₄ 4⁻² - 3log₄ 4¹/² =3-(-2)-3*(1/2)=3+2-1.5=3.5
9.
tg(3π/4)=tg(4π/4 - π/4) = -tg(π/4)=-1
cos(5π/3)=cos(6π/3 - π/3) =cos(π/3)=1/2
sin(7π/6)=sin(6π/6 + π/6)=-sin(π/6)=-1/2
sin(2π/3)=sin(3π/3 - π/3) = sin (π/3)=√3/2
-1+(1/2)*(-1/2)-(√3/2)²=-1-(1/4)-(3/4)=-1-1=-2
10.
(1/4)^x + (1/4)^(x-1)>5
(1/4)^x (1+(1/4)⁻¹)>5
(1/4)^x (1+4)>5
(1/4)^x * 5>5
(1/4)^x>1
(1/4)^x >(1/4)⁰
x<0
liska16:
А можно пожалуйста решение, если вас не затруднит)))
Решения даны.
Автор ответа:
1
Похожие вопросы
Предмет: Русский язык,
автор: настя7751
Предмет: Другие предметы,
автор: Mishytka1998
Предмет: Русский язык,
автор: orynbekovmagzhan
Предмет: Другие предметы,
автор: ilyablagov
Предмет: Биология,
автор: ilyablagov