Предмет: Математика,
автор: GROFPNW
№322 СРОЧНО!!!!! ЗАРАНЕЕ СПАСИБО !
Приложения:
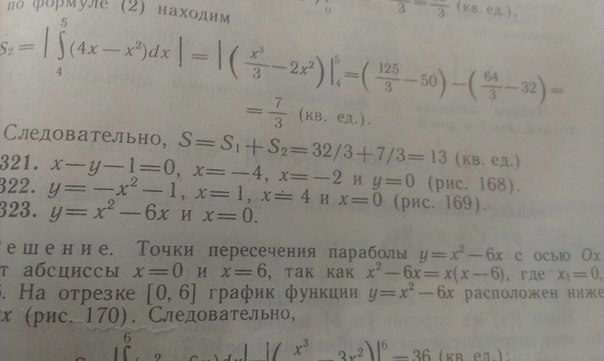
Ответы
Автор ответа:
1
Криволинейная трапеция- фигура, расположенная в первой четверти.
В данном случае фигура расположена в четвертой четверти.
Но площадь данной фигуры в точности равна площади криволинейной трапеции расположенной в первой четверти и ограниченной осью ох ( у=0)
прямыми х=1 и х=4 и кривой у = х²+1
Поэтому решение такое

Или по правилу

В данном случае фигура расположена в четвертой четверти.
Но площадь данной фигуры в точности равна площади криволинейной трапеции расположенной в первой четверти и ограниченной осью ох ( у=0)
прямыми х=1 и х=4 и кривой у = х²+1
Поэтому решение такое
Или по правилу
Похожие вопросы
Предмет: Русский язык,
автор: zerolya
Предмет: Русский язык,
автор: Шамиль5класс
Предмет: Английский язык,
автор: Аноним
Предмет: Химия,
автор: frih
Предмет: Оʻzbek tili,
автор: xadicha1984