Предмет: Алгебра,
автор: nadtgh
ПОМОГИТЕ РЕШИТЬ НЕРАВЕНСТВО!!
Приложения:
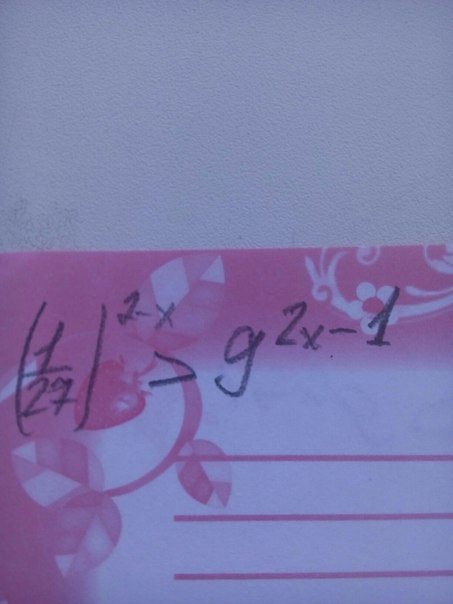
Ответы
Автор ответа:
1
NNNLLL54:
2(2-x)=4-2x ....
По условию 2(2х-1)=4х-2
Автор ответа:
1
Похожие вопросы
Предмет: Русский язык,
автор: Nina1911
Предмет: Русский язык,
автор: Димоноооооооооо
Предмет: Окружающий мир,
автор: Anjowunk
Предмет: Английский язык,
автор: Аноним
Предмет: Литература,
автор: eroptank