Предмет: Математика,
автор: anytarur
Вычислить определенный интеграл
Приложения:
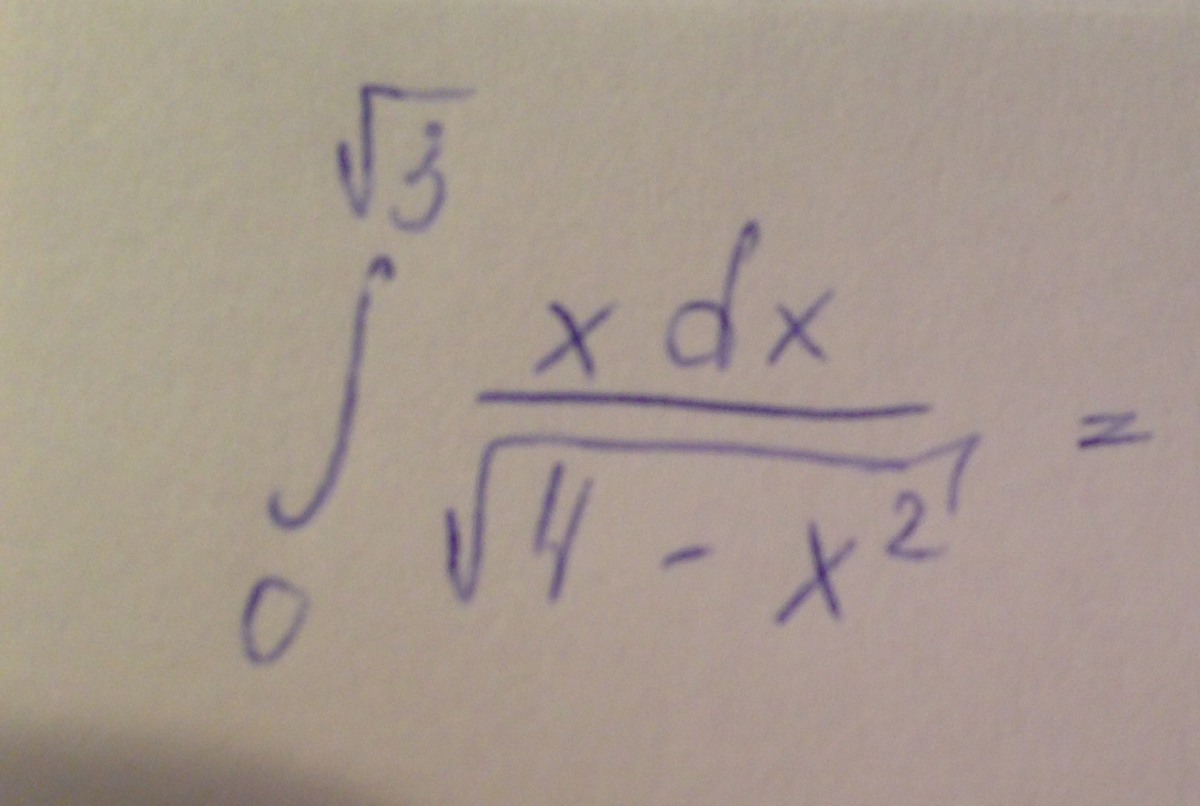
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Русский язык,
автор: Bukvar2006
Предмет: Английский язык,
автор: КыРгЫз2002
Предмет: Другие предметы,
автор: Decerneyrer
Предмет: Математика,
автор: valeria741
Предмет: Математика,
автор: jisoo21