Предмет: Математика,
автор: tsisangulova
решите пожалуйста дифференциальные уравнения
Приложения:
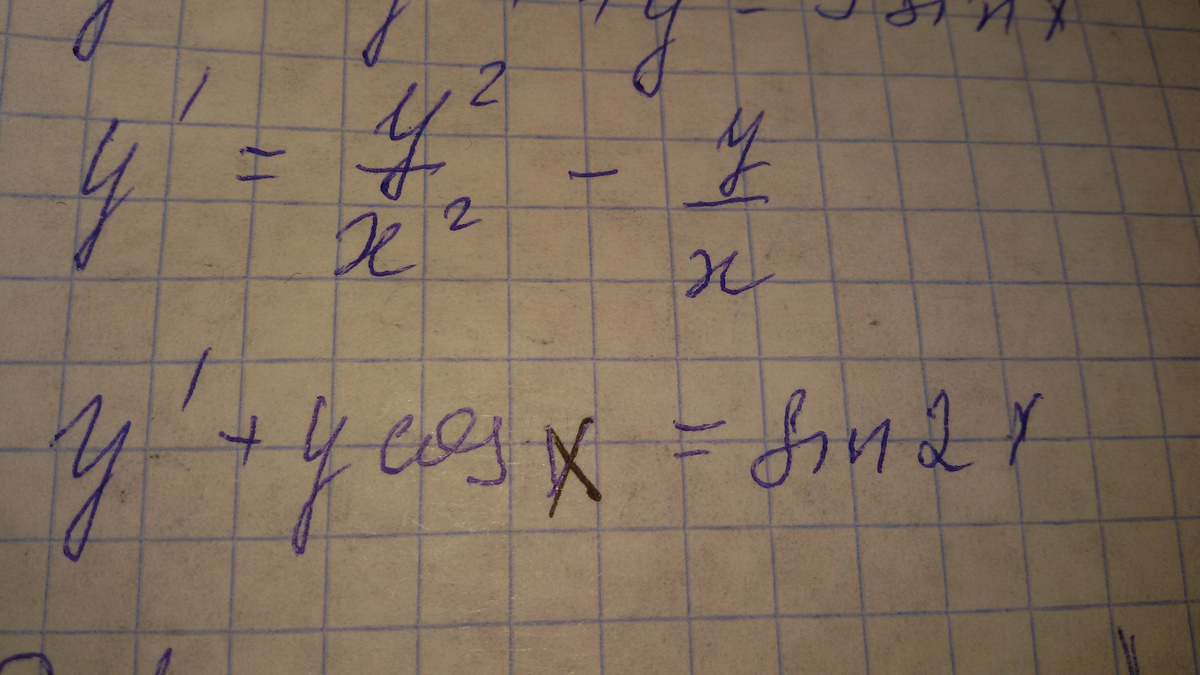
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Русский язык,
автор: jsjd
Предмет: Русский язык,
автор: LyaLya2007
Предмет: Русский язык,
автор: 333399
Предмет: Алгебра,
автор: Lalalupci
Предмет: Математика,
автор: Аноним