Предмет: Алгебра,
автор: TETRIS24
1)Дана функция  . Найдите координаты точек её графика, в которых касательные к нему параллельны оси абсцисс.
. Найдите координаты точек её графика, в которых касательные к нему параллельны оси абсцисс.
2).Решите уравнение во вложении
3)Решите неравенство 
помогите с алгеброй распишите подробно напишите
на листе или в латеске.
в простом виде непонятно
Приложения:
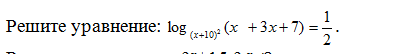
Аноним:
Там в логарифме x^2+3x+7 ?
условие в картинке
Да, но просто там нет квадрата. Что очень странно.
я сделал скрин задания
Ну ладно, как написано, так написано.
квадрат есть
х+10 ^2
в скобках
Я про: x+3x+7
а там нету
Ответы
Автор ответа:
2
Касательная параллельна оси абсцисс в точках минимума или максимума, то есть тогда, тогда производная этой функции равна 0.
Искомые точки:
2) Во вложении.
Метод интервалов:
Приложения:

Похожие вопросы
Предмет: Русский язык,
автор: vova9889
Предмет: Другие предметы,
автор: altushkina163
Предмет: Английский язык,
автор: илья1862
Предмет: Английский язык,
автор: akhvayanp5jie3
Предмет: Алгебра,
автор: Аноним