Предмет: Геометрия,
автор: kvast
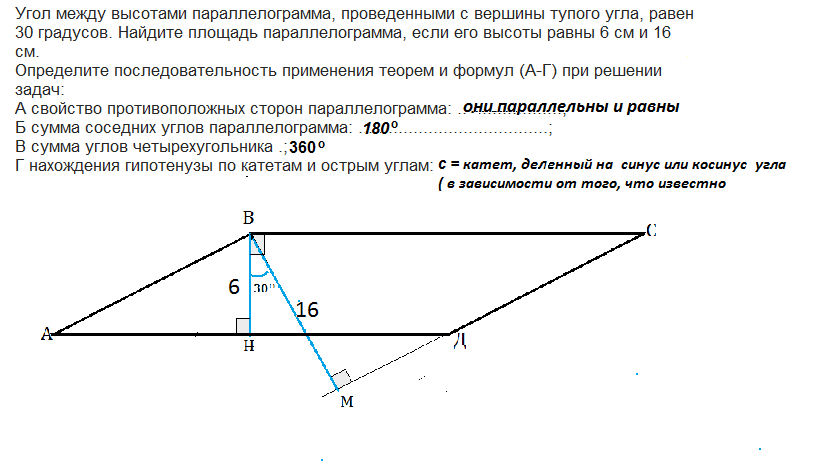
Очень нужно, учительница требует на все вопросы ответ. Угол между высотами параллелограмма, проведенными с вершины тупого угла, равен 30 градусов. Найдите площадь параллелограмма, если его высоты равны 6 см и 16 см.
Определите последовательность применения теорем и формул (А-Г) при решении задач:
А свойство противоположных сторон параллелограмма: .....................;
Б сумма соседних углов параллелограмма: ......................................;
В сумма углов четырехугольника .;
Г нахождения гипотенузы по катетом и острым углом: Заранее спасибо. Пожалуйста с объячнением
Ответы
Автор ответа:
0
Обозначим вершины параллелограмма АВСД.
Соразмерно условию сделаем и рассмотрим рисунок.
Противоположные стороны параллелограмма параллельны и равны.
Высота параллелограмма перпендикулярна его противоположным сторонам.
ВН ⊥ ВС и ⊥ АД
ВМ ⊥ АВ и ⊥ прямой, содержащей СД ⇒
Угол АВМ - прямой, угол АВН=90º-60º, ⇒
угол ВАН=30º
Противоположные углы параллелограмма равны. ⇒
угол ВСД= углу ВАД=30º
Катет ВН в треугольнике АВН противолежит углу 30º.
Гипотенуза в два раза больше катета, противолежащего углу 30º.
АВ=ВН:sin (30º)=6: 0,5=12 см
Катет ВМ в треугольнике ВСМ противолежит углу 30º.
ВС=ВМ:sin (30º)=16: 0,5=32 см
Площадь параллелограмма равна произведению его высоты на сторону, к которой она проведена.
S АВСД=6*32=192 см²илиS АВСД=16*12=192 см²
или
S АВСД=16*12=192 см²
Соразмерно условию сделаем и рассмотрим рисунок.
Противоположные стороны параллелограмма параллельны и равны.
Высота параллелограмма перпендикулярна его противоположным сторонам.
ВН ⊥ ВС и ⊥ АД
ВМ ⊥ АВ и ⊥ прямой, содержащей СД ⇒
Угол АВМ - прямой, угол АВН=90º-60º, ⇒
угол ВАН=30º
Противоположные углы параллелограмма равны. ⇒
угол ВСД= углу ВАД=30º
Катет ВН в треугольнике АВН противолежит углу 30º.
Гипотенуза в два раза больше катета, противолежащего углу 30º.
АВ=ВН:sin (30º)=6: 0,5=12 см
Катет ВМ в треугольнике ВСМ противолежит углу 30º.
ВС=ВМ:sin (30º)=16: 0,5=32 см
Площадь параллелограмма равна произведению его высоты на сторону, к которой она проведена.
S АВСД=6*32=192 см²илиS АВСД=16*12=192 см²
или
S АВСД=16*12=192 см²
Приложения:
Автор ответа:
0
ВК=6 см - высота;
ВМ=16 см - высота;
КВМ=30°;
S - ?
ВСМ - прямоугольный треугольник;
МВС=90-30=60°;
ВС=АД=16/cos60°=16/1/2=32 см;
S=АД/ВК=32*6=192 см².
А - противоположные стороны параллелограмма равны и параллельны;
Б - сумма соседних углов параллелограмма 180°;
В - сумма углов четырехугольника 360°;
Г - гипотенуза равна катет умножить на косинус или синус угла (в зависимости от того какой угол дан).
ВМ=16 см - высота;
КВМ=30°;
S - ?
ВСМ - прямоугольный треугольник;
МВС=90-30=60°;
ВС=АД=16/cos60°=16/1/2=32 см;
S=АД/ВК=32*6=192 см².
А - противоположные стороны параллелограмма равны и параллельны;
Б - сумма соседних углов параллелограмма 180°;
В - сумма углов четырехугольника 360°;
Г - гипотенуза равна катет умножить на косинус или синус угла (в зависимости от того какой угол дан).
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: пярьиос
Предмет: Английский язык,
автор: AZIKOSHA
Предмет: Другие предметы,
автор: 12123456789
Предмет: Математика,
автор: galina19792012