Предмет: Математика,
автор: jurecRok
Равнобочная трапеция с основаниями 12 см и 18 см и высотой 4 см вращается около большого основания . Найдите объем тела вращения .
Ответы
Автор ответа:
16
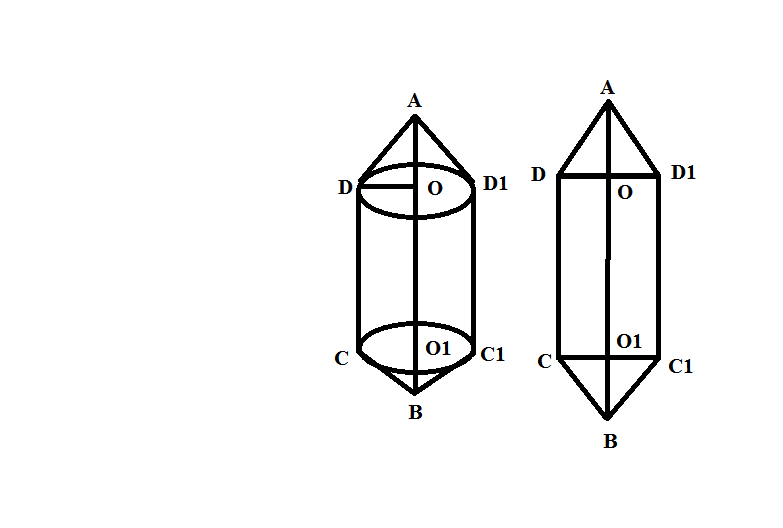
Тело вращения - цилиндр с добавленными к основаниям конусами.
Vтела=V цил. + 2V конусов
Vцил=πR²h, h цил.=12cм; R=4cм
Vцил=π4²*12=192π(см³)
Vконуса=1/3πR²h, h конуса=(18-12):2=3(cм), R=4cм
2Vконусов=2/3*4²*3π=32π(см³)
Vтела=192π+32π=224π(см³)≈703,36(см³)
Vтела=V цил. + 2V конусов
Vцил=πR²h, h цил.=12cм; R=4cм
Vцил=π4²*12=192π(см³)
Vконуса=1/3πR²h, h конуса=(18-12):2=3(cм), R=4cм
2Vконусов=2/3*4²*3π=32π(см³)
Vтела=192π+32π=224π(см³)≈703,36(см³)
Автор ответа:
2
Смотреть рисунок в приложении. Полученное тело вращения можно разбить на два равных конуса и цилиндр. Так как высота трапеции будет являться радиусами оснований цилиндров и конуса, то площадь основания конуса и цилиндра равна: 16π см². Меньшее основание трапеции будет являться высотой цилиндра, значит, объем цилиндра равен: 16π * 12 =192π см³. Так как высота конуса будет равна полуразности оснований: (18-12)\2= 3 см, то его объем равен  см³. Значит, объем всего тела равен: 2*16π + 192π= 224π см³
см³. Значит, объем всего тела равен: 2*16π + 192π= 224π см³
Приложения:
Похожие вопросы
Предмет: Окружающий мир,
автор: Аноним
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: wolchonoklina
Предмет: Математика,
автор: 210681
Предмет: Русский язык,
автор: otto223199