Предмет: Алгебра,
автор: Toder
Найти производную Помогите
Приложения:
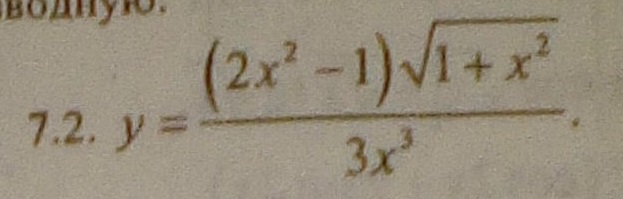
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Русский язык,
автор: dvoeshnik101
Предмет: Русский язык,
автор: пипл5
Предмет: Другие предметы,
автор: дашуля0901
Предмет: Алгебра,
автор: Burlovadsria
Предмет: Алгебра,
автор: Аноним