Question

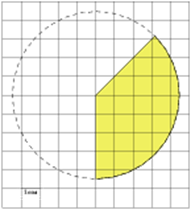
Найдите (в см2) площадь фигуры, изображенной на клетчатой бумаге с размером клетки 1 см × 1 см.
(Для того, чтобы найти радиус окружности, определите, в каких точках окружность проходит через пересечения линий сетки.)

Answer 1

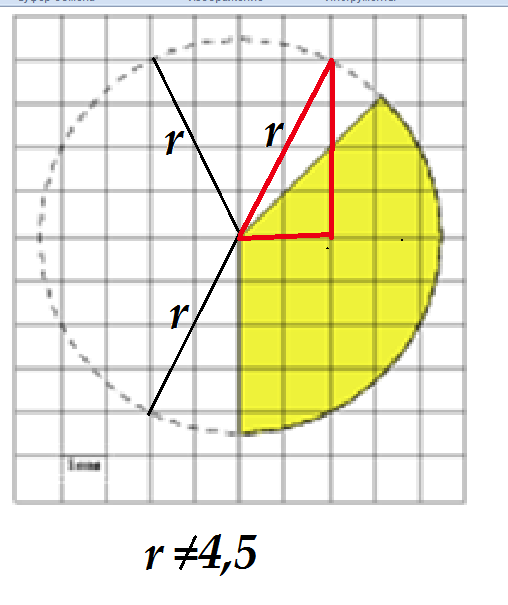
На рисунке закрашен сектор круга. Для нахождения его площади пользуемся формулой: 0.5*p*r, где p - длина дуги, заключенной между радиусами, а r - радиус. По рисунку (см. приложение) видно, что радиус равен $\sqrt{4+16} = 2\sqrt{5}$ см, а длину дуги найдем по формуле: (πrα)\180°, где α - центральный угол. По рисунку видно, что угол α = 90°+45°= 135°. Значит, длина дуги равна: (2√5*135*π)\180 = 1,5√5π. Найдем площадь сектора: 0,5*1,5√5π*2√5=7,5π см²
Ответ: 7,5π см²