№1 Найдите площадь параллелограмм, если две его стороны 1) 12 и 11, 2) 40 и 10, 3) 7 и 5, 23 и 11, 4) 9 и 14, а угол между ними равен 30 градусов. №2 Найдите площадь ромба, если его стороны равны 1) 14, 2) 5, 3) 27, 4) 13, а один из углов равен 150 градусов.
Ответы
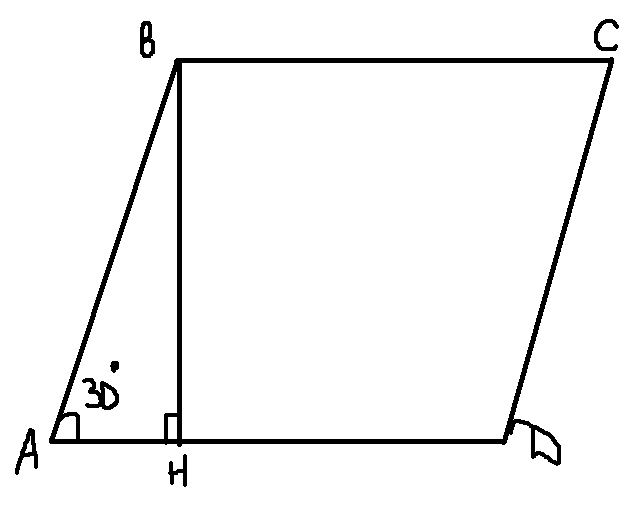
Параллелограмм:
1)
AB=11
AD=12
угол A = 30
Проводим высоту BH.
Рассм. тр. ABH - угол Н=90, угол A = 30, значит угол B=60. отсюда следует, что BH=1/2AB
BH=1/2*11=5.5
S=a*h
S=12*5.5 = 66
2)
AB=10
AD=40
угол A = 30
Проводим высоту BH.
Рассм. тр. ABH - угол Н=90, угол A = 30, значит угол B=60. отсюда следует, что BH=1/2AB
BH=1/2*10=5
S=a*h
S=40*5= 200
3)
AB=5
AD=7
угол A = 30
Проводим высоту BH.
Рассм. тр. ABH - угол Н=90, угол A = 30, значит угол B=60. отсюда следует, что BH=1/2AB
BH=1/2*5=2.5
S=a*h
S=7*2.5 = 17.5
4)
AB=11
AD=23
угол A = 30
Проводим высоту BH.
Рассм. тр. ABH - угол Н=90, угол A = 30, значит угол B=60. отсюда следует, что BH=1/2AB
BH=1/2*11=5.5
S=a*h
S=23*5.5 = 126.5
5)
AB=9
AD=14
угол A = 30
Проводим высоту BH.
Рассм. тр. ABH - угол Н=90, угол A = 30, значит угол B=60. отсюда следует, что BH=1/2AB
BH=1/2*9=4.5
S=a*h
S=14*4.5 = 77
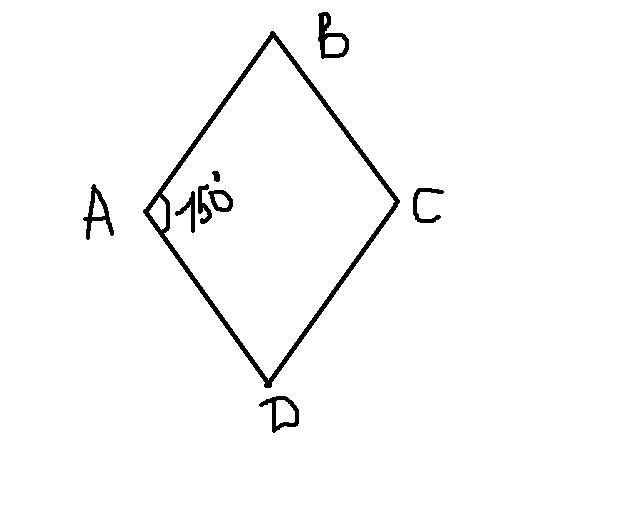
Ромб:
1)
угол A = 150
AB = 14
угол A = углу В = 150
угол B = углу С = (360-150-150)/2 = 30
S=a²*Sinβ
S=14²*Sin30=196*(1/2)=98
2)
угол A = 150
AB = 5
угол A = углу В = 150
угол B = углу С = (360-150-150)/2 = 30
S=a²*Sinβ
S=5²*Sin30=25*(1/2)=12.5
3)
угол A = 150
AB = 27
угол A = углу В = 150
угол B = углу С = (360-150-150)/2 = 30
S=a²*Sinβ
S=27²*Sin30=729*(1/2)=364.5
4)
угол A = 150
AB = 13
угол A = углу В = 150
угол B = углу С = (360-150-150)/2 = 30
S=a²*Sinβ
S=13²*Sin30=169*(1/2)=84.5