Предмет: Геометрия,
автор: Alla0204
Три кола радіусами 2, 3 і 10 ПОПАРНО дотикаються зовні. Знайти радіус кола, яке вписано в трикутник, утворений центрами цих кіл.
Ответы
Автор ответа:
14
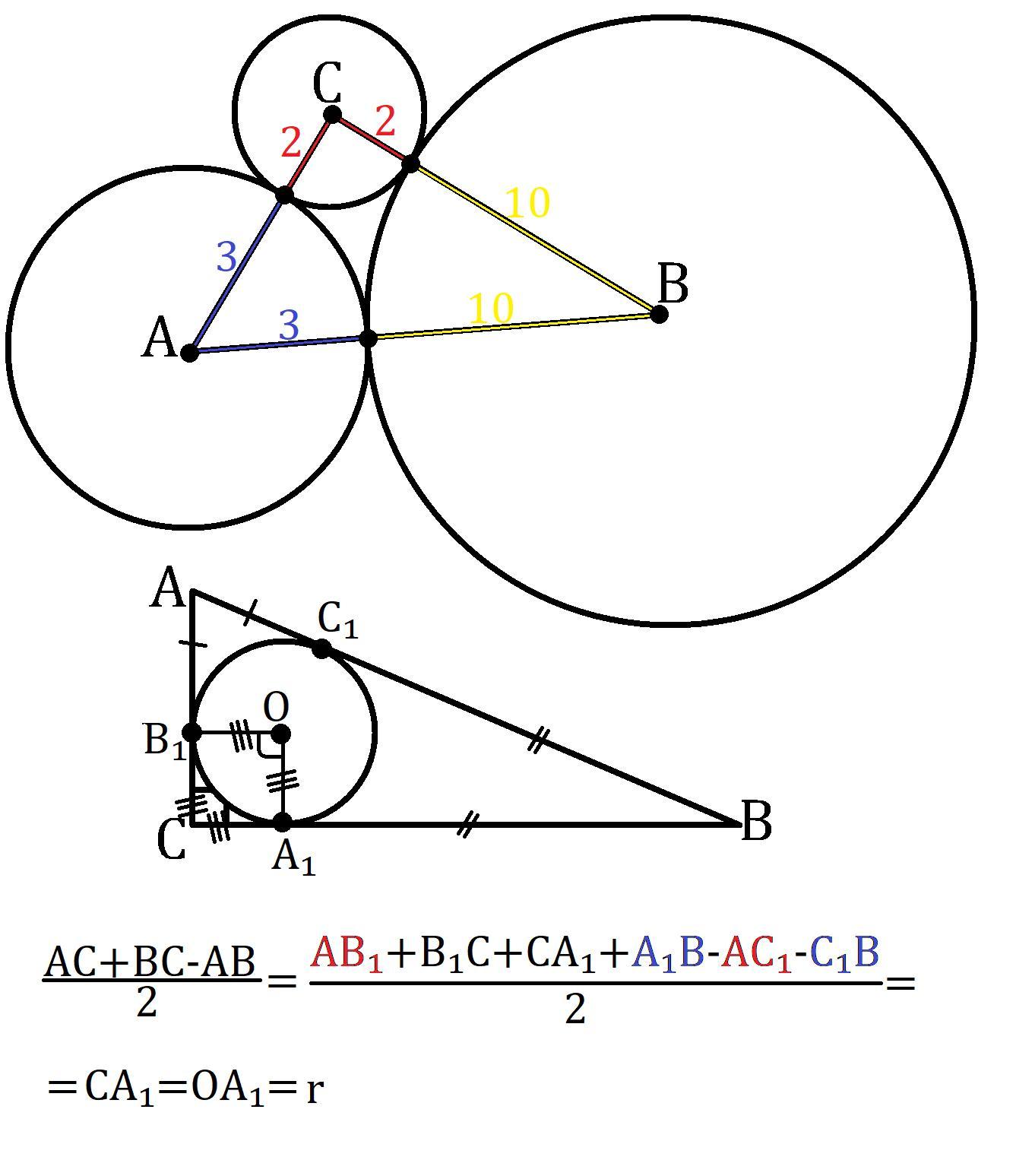
Точка касаниях двух окружностей и их центры лежат на одной прямой, поэтому ΔABC, c вершинами в центрах окружностей, имеет стороны AC=3+2=5, CB=2+10=12, BA=10+3=13.
Рассмотрим ΔABC:
AC=5, BC=12, AB=13. Числа 5, 12 и 13 составляют Пифагорову тройку, поэтому угол лежащий напротив стороны равной 13 - прямой. ∠C=90°.
В прямоугольном треугольнике радиус вписанной равен полуразности суммы катетов и гипотенузы (объяснение внизу).
r = (AC+BC-AB):2 = (5+12-13):2 = 4:2 = 2
Ответ: 2.
Приложения:
Похожие вопросы
Предмет: Другие предметы,
автор: ГасановаЗалина
Предмет: Русский язык,
автор: nvgokov
Предмет: Английский язык,
автор: shukhrat89
Предмет: Русский язык,
автор: jan2110
Предмет: Биология,
автор: olessiashavlokhova