Предмет: Математика,
автор: Eugena
Помогите, пожалуйста, решить
Приложения:
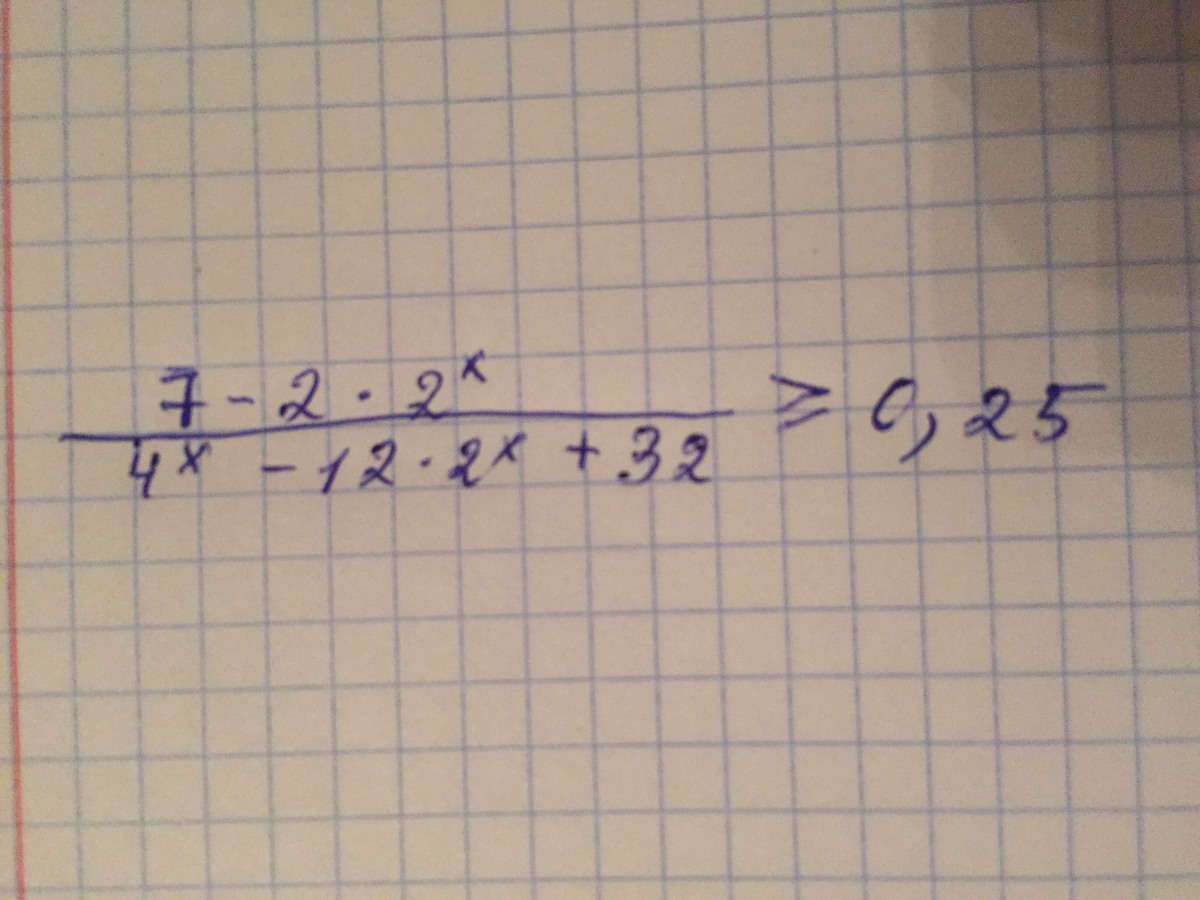
Ответы
Автор ответа:
0
введем замену
D=144-128=16
t1=8
t2=4
решаем методом интервалов
наносим на числовую прямую t=2 - закрашена, остальные выколоты, так как знаменатель не равен нулю
t∈ {2} (4;8)
Ответ: {1} (2;3)
Похожие вопросы
Предмет: Английский язык,
автор: vika3637
Предмет: Английский язык,
автор: ls300503
Предмет: Українська мова,
автор: desimero
Предмет: Английский язык,
автор: MyliukovaAnna001
Предмет: Русский язык,
автор: U1yaSverd10va