Предмет: Геометрия,
автор: gunka00009
Площадь боковой поверхности конуса равна 60пи см^2. Расстояние от центра основания до образующей равна 4,8 см. Найти объем конуса.
Ответы
Автор ответа:
4
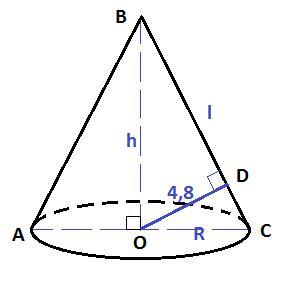
Дано : конус, OC = OA = R, BA = BC = - образующие,
Sбок = 60π см² , OD⊥BC, OD = 4,8 см
Найти : V
Решение :
BO = h - высота конуса, ΔВОС - прямоугольный
ΔВОС ~ ΔВDО по общему острому углу ∠OBD
Sбок =
Объём конуса
Ответ : 96π см³
Приложения:
Похожие вопросы
Предмет: Немецкий язык,
автор: Spamm
Предмет: Русский язык,
автор: BLACKEDcom
Предмет: Окружающий мир,
автор: Никнепридумала
Предмет: Математика,
автор: sunzvezdochka
Предмет: Английский язык,
автор: 12345vgd