Предмет: Алгебра,
автор: kakchtodealt
Как решить данное уравнение?
Приложения:
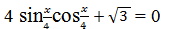
Ответы
Автор ответа:
1
Это уравнение с помощью формулы синуса двойного угла сводится к простейшему тригонометрическому уравнению, решение которого находится по формуле.


Похожие вопросы
Предмет: Українська мова,
автор: NazariyUA
Предмет: Русский язык,
автор: t1611899
Предмет: Русский язык,
автор: t1611899
Предмет: Литература,
автор: popenko2403
Предмет: Немецкий язык,
автор: lulu6880