Предмет: Математика,
автор: dezy
Решите пожалуйста , очень надо
Приложения:
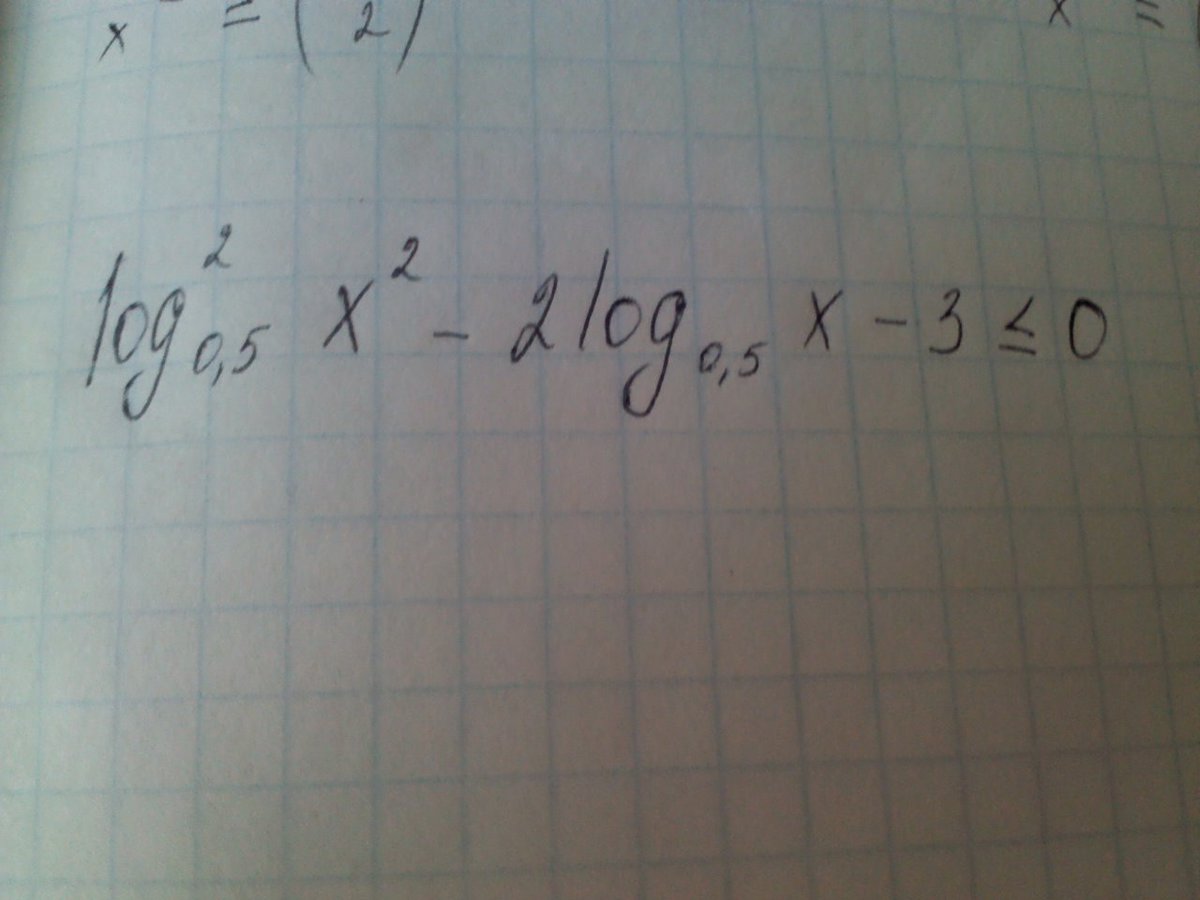
Ответы
Автор ответа:
1
введем замену
D=4+48=52
решаем методом интервалов и получаем
t∈[
Ответ:[
Похожие вопросы
Предмет: Русский язык,
автор: Valeramatvievs
Предмет: Английский язык,
автор: lnna130512
Предмет: Українська мова,
автор: Vladolis
Предмет: Французский язык,
автор: PecHnKa2006
Предмет: Українська мова,
автор: vasyaua1