Question

Найти площадь фигуры расположенной в 1 четверти и ограниченной линиями y=12x^3 y= -24x^2+36x

Answer 1

$S= \int\limits^1_0 {(-24 x^{2} +36x-12 x^{3}) } \, dx =( -3x^{4}-8 x^{3}+18 x^{2} )| _{0} ^{1} = \\ =(-3-8+18)=7$

Answer 2

Найдем пределы интегрирования
12x³=-24x²+36x
12x³+24x²-36x=0
12x(x²+2x-3)=0
x=0
x²+2x-3=0
x1+x2=-2 U x1*x2=-3
x1=-3-не удов.усл,т.к.фигура расположена в 1 ч
x2=1
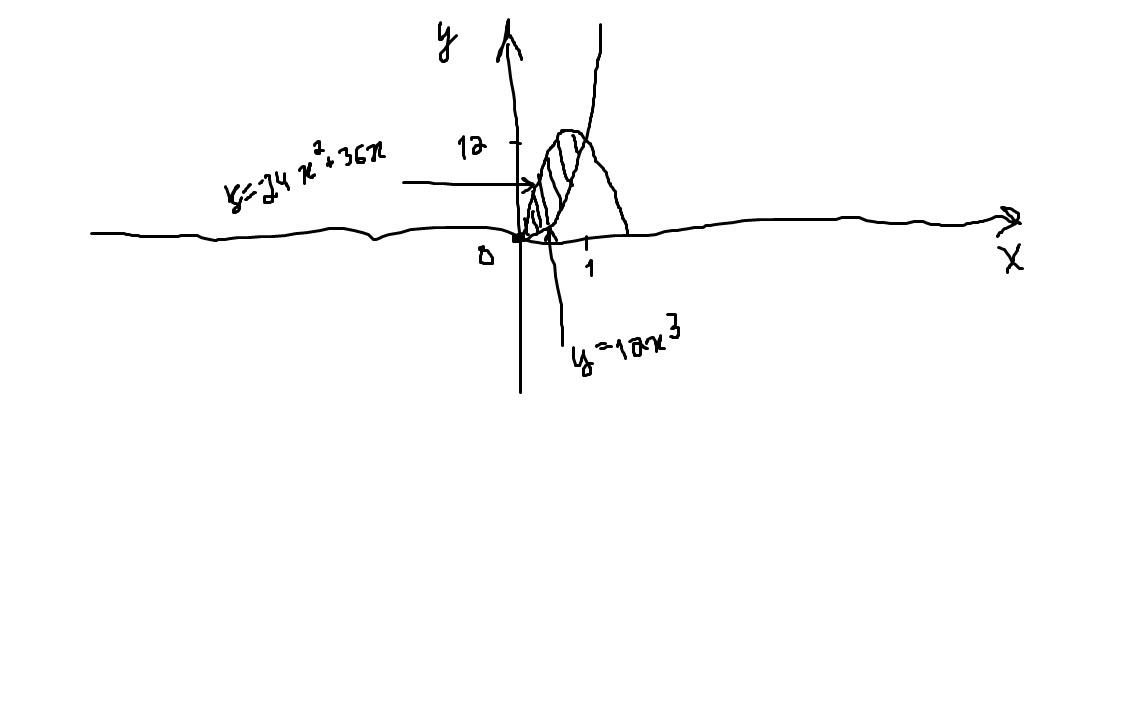
y=12x³ кубическая парабола
у=-24х²+36х квадратная парабола,ветви вниз
Фигура ограничена сверху графиком у=-24х²+36х,а снизу графиком у=12х³
$S= \int\limits^1_0 {(-24x^2+36x-12x^3)} \, dx =-8x^3+18x^2-3x^4=-8+18-3=7$

51a61b0113bb58d17afa695de9ad1cce.docx