Предмет: Алгебра,
автор: ahundova777
РЕБЯТ 100 БАЛЛОВ!!!
Помогите доделать.
Преподователю нужно доделать, а я не понимаю вообще..
Чтобы найти максимальное или минимальное значение на отрезке надо:
1) найти точки критические (приравнять производную к 0)
2) выбрать те из них, которые принадлежат промежутку
3) вычислить значения функции на концах и в найденных критических точках
4) выбрать минимально/максимальное значения
Вы нашли только значение в критической точке, а про концы отрезка забыли.
Приложения:
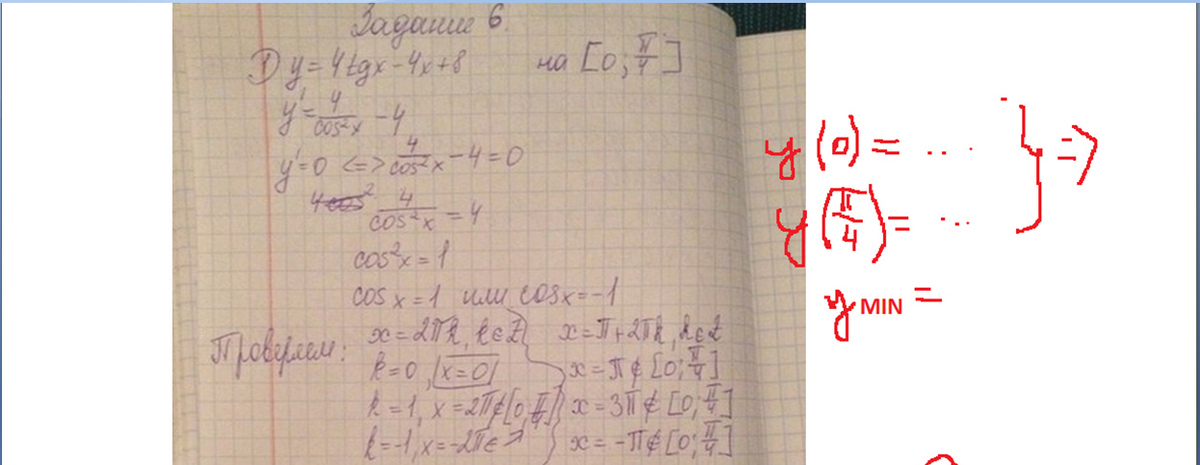

Ответы
Автор ответа:
2
№2



 или
или 
нет корней x=12

 - наименьшее
- наименьшее
 - наибольшее
- наибольшее
e≈0.4
№1





 или
или 
 k∈Z или
k∈Z или  n∈Z
n∈Z



из 1) случая k=0 x=0
из 2) таких x принадлежащих отрезку нет
 - наименьшее
- наименьшее
 - наибольшее
- наибольшее
π≈3.14
нет корней x=12
e≈0.4
№1
из 1) случая k=0 x=0
из 2) таких x принадлежащих отрезку нет
π≈3.14
Автор ответа:
1
смотреть во вложении
Приложения:

Похожие вопросы
Предмет: Русский язык,
автор: ВероеикаМакарова
Предмет: Русский язык,
автор: alinahm
Предмет: Русский язык,
автор: cpocht
Предмет: Русский язык,
автор: 12345674069
Предмет: Английский язык,
автор: nomokonjar