Предмет: Алгебра,
автор: Вика901
помогите пожалуйста только 1 задание
Приложения:

zakinyan1:
Какое именно? Поподробнее, пожалуйста)
1) а, б, в ???
да
ок
Ответы
Автор ответа:
1
а 1 точно правильно?
там же 8-15x^2
y(1)=8-15*(1)^2
разве не так?
там же 8-15x^2
y(1)=8-15*(1)^2
разве не так?
так, но это и есть 8-15=-7
спасибо:*
Автор ответа:
1
1) 
2 и 3 задание смотри во вложении
2 и 3 задание смотри во вложении
Приложения:
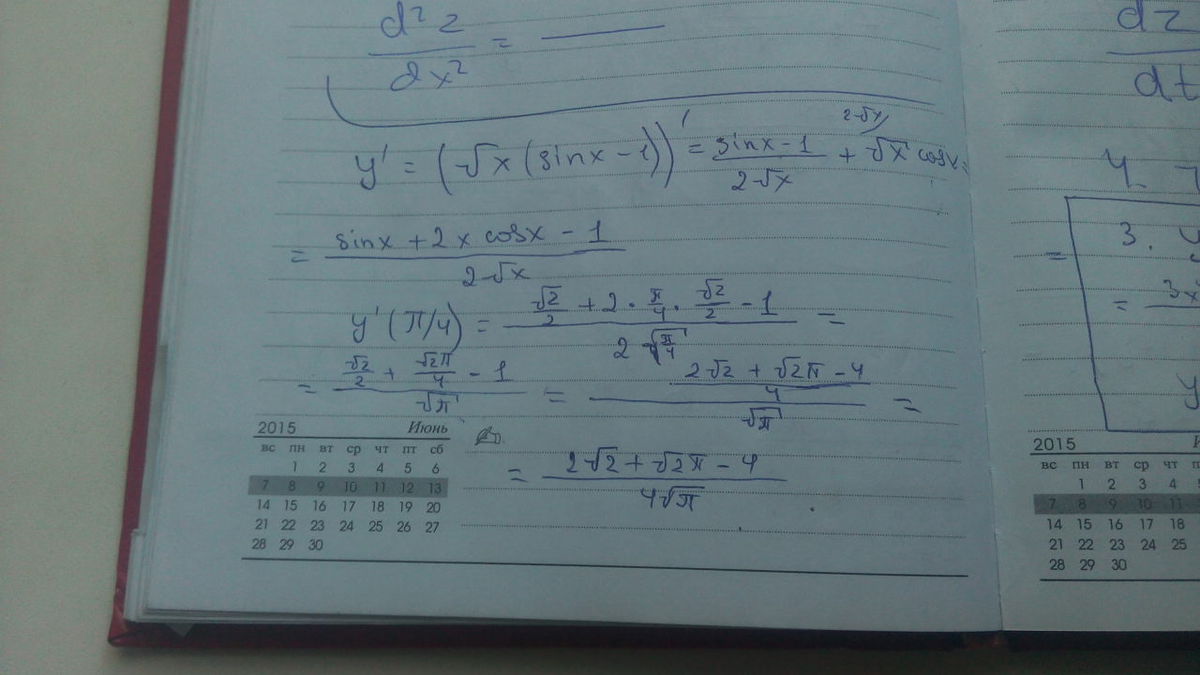

Спасибо тебе:*
Всегда рад помочь ;-)
Похожие вопросы
Предмет: Английский язык,
автор: Mary15072004
Предмет: Русский язык,
автор: oktemba851
Предмет: Русский язык,
автор: katypisareva1
Предмет: Алгебра,
автор: amina20055687