Question

1. У прямой правильной призмы в три раза уменьшили сторону квадратного основания и в два раза уменьшили высоту. Определить, во сколько раз изменился ее объем.

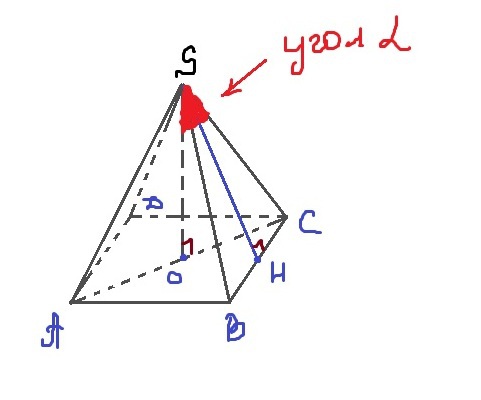
2. Дана правильная четырехгранная пирамида. Сторона основания равна 8. Апофема равна 12. Найти угол между боковым ребром и высотой пирамиды.

Answer 1

1) Обозначим сторону основания (квадрата) буквой $a$, $h$ - высоту.
$V$ призмы=$S$ осн.$*h$
В нашем случае: $V=a^2h$

После уменьшения величин:

$V=( \frac{a}{3} )^2* \frac{h}{2} = \frac{a^2}{9} *\frac{h}{2}= \frac{a^2h}{18}$

Сравним былой объем и ставший:

$\frac{V_1}{V_2} = \frac{a^2h}{ \frac{a^2h}{18} } =18$

Ответ: Объем уменьшился в $18$ раз

2) Смотрим рисунок.
Рассмотрим Δ$SHC:$
$SC= \sqrt{144+16} = \sqrt{160} =4 \sqrt{10}$  -  по теореме Пифагора.

Рассмотрим Δ$ABC:$
$AC= \sqrt{8^2+8^2} = \sqrt{8^2*2} =8 \sqrt{2} \\ OC=4 \sqrt{2}$

Рассмотрим Δ$SOC:$
$SO= \sqrt{(4 \sqrt{10})^2-(4 \sqrt{2} )^2 } = \sqrt{160-32} = \sqrt{128} = \sqrt{64*2} =8 \sqrt{2}$
$tg \alpha = \frac{OC}{SO} = \frac{4 \sqrt{2} }{8 \sqrt{2} } = \frac{1}{2} \\ \\ \alpha =arctg \frac{1}{2}$

Ответ: $arctg \frac{1}{2}$

Answer 2

V=Sосн*h
пусть x - сторона основания, h - высота
V=x²*h
$\frac{x}{3}$ - новая сторона
$\frac{h}{2}$ - новая высота
$V_{1} = \frac{x^2}{9}* \frac{h}{2} = \frac{x^2*h}{18}$
$\frac{V}{ V_{1} } = {x^2*h}: \frac{x^2*h}{18} =18$
Ответ в 18 раз

№ 2 
<OSC - искомый
OS - высота
ABCD  - квадрат, значит AB=8
OK=1/2*8=4
SOK - прямоугольный по теореме Пифагора
SO=$\sqrt{12^2-4^2}= \sqrt{144-16}=8 \sqrt{2}$
OC=4√2
$\frac{OK}{SO}= tg \ \textless \ OSK$
$\frac{4\sqrt{2}}{8 \sqrt{2} } =tg \ \textless \ OSK$
< OSK= arctg $\frac{1}{2 } }$