Предмет: Алгебра,
автор: Prikolist5221
Найти точку минимума/максимума функции.
Приложения:
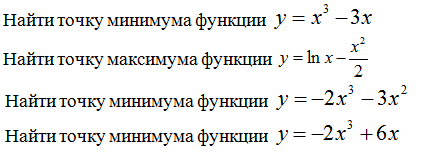
Ответы
Автор ответа:
0
Находим первую производную функции:
y' = 3x²-3
Приравниваем ее к нулю:
3x²-3 = 0
x1 = -1
x2 = 1
Вычисляем значения функции
f(-1) = 2
f(1) = -2
Найдем вторую производную:
y'' = 6x
y''(-1) = -6<0 - значит точка x = -1 точка максимума функции.
y''(1) = 6>0 - значит точка x = 1 точка минимума функции.

Находим первую производную функции:
y' = (-x²+1)/x
Приравниваем ее к нулю:
-x+1/x = 0
x1 = -1
x2 = 1
Вычисляем значения функции
f(-1) = -1/2+I•π
f(1) = -1/2
y'' = -x²-1/x2
y''(-1) = -2<0 - значит точка x = -1 точка максимума функции.
y''(1) = -2<0 - значит точка x = 1 точка максимума функции.

y' = 6x(-x-1)
Приравниваем ее к нулю:
-6x²-6x = 0
x1 = -1
x2 = 0
Вычисляем значения функции
f(-1) = -1
f(0) = 0
Найдем вторую производную:
y'' = -12x-6
y''(-1) = 6>0 - значит точка x = -1 точка минимума функции.
y''(0) = -6<0 - значит точка x = 0 точка максимума функции.

Находим первую производную функции:
y' = -6x²+6
Приравниваем ее к нулю:
x1 = -1
x2 = 1
Вычисляем значения функции
f(-1) = -4
f(1) = 4
Найдем вторую производную:
y'' = -12x
y''(-1) = 12>0 - значит точка x = -1 точка минимума функции.
y''(1) = -12<0 - значит точка x = 1 точка максимума функции.
y' = 3x²-3
Приравниваем ее к нулю:
3x²-3 = 0
x1 = -1
x2 = 1
Вычисляем значения функции
f(-1) = 2
f(1) = -2
Найдем вторую производную:
y'' = 6x
y''(-1) = -6<0 - значит точка x = -1 точка максимума функции.
y''(1) = 6>0 - значит точка x = 1 точка минимума функции.
Находим первую производную функции:
y' = (-x²+1)/x
Приравниваем ее к нулю:
-x+1/x = 0
x1 = -1
x2 = 1
Вычисляем значения функции
f(-1) = -1/2+I•π
f(1) = -1/2
y'' = -x²-1/x2
y''(-1) = -2<0 - значит точка x = -1 точка максимума функции.
y''(1) = -2<0 - значит точка x = 1 точка максимума функции.
y' = 6x(-x-1)
Приравниваем ее к нулю:
-6x²-6x = 0
x1 = -1
x2 = 0
Вычисляем значения функции
f(-1) = -1
f(0) = 0
Найдем вторую производную:
y'' = -12x-6
y''(-1) = 6>0 - значит точка x = -1 точка минимума функции.
y''(0) = -6<0 - значит точка x = 0 точка максимума функции.
Находим первую производную функции:
y' = -6x²+6
Приравниваем ее к нулю:
x1 = -1
x2 = 1
Вычисляем значения функции
f(-1) = -4
f(1) = 4
Найдем вторую производную:
y'' = -12x
y''(-1) = 12>0 - значит точка x = -1 точка минимума функции.
y''(1) = -12<0 - значит точка x = 1 точка максимума функции.
Автор ответа:
0
1) 

+ -1 - 1 +
Ответ:
2)

- -1 + 1 -
Ответ:
3)

- -1 + 0 -
Ответ:
4)

- -1 + 1 -
Ответ:
+ -1 - 1 +
Ответ:
2)
- -1 + 1 -
Ответ:
3)
- -1 + 0 -
Ответ:
4)
- -1 + 1 -
Ответ:
Похожие вопросы
Предмет: Английский язык,
автор: MSchumacher21
Предмет: Другие предметы,
автор: mirov0010
Предмет: Русский язык,
автор: Галинака
Предмет: Русский язык,
автор: stasik20023