Предмет: Информатика,
автор: alicecarroll
Определите, при каком наименьшем значении b в результате выполнения следующего алгоритма будет напечатано число 15.
Ответ есть, но нигде не могу найти принцип решения, объясните кто-нибудь, пожалуйста.
Приложения:

Ответы
Автор ответа:
1
печатать 14 будет последний раз при В = F(15-1)+8 или
8+8...8= 14 раз по 8 = 112
Если В = 112 то будет печатать 14
Увеличим В на 1, т.е. В=113 будет печатать 15.
Это рекурсия.
8+8...8= 14 раз по 8 = 112
Если В = 112 то будет печатать 14
Увеличим В на 1, т.е. В=113 будет печатать 15.
Это рекурсия.
Приложения:
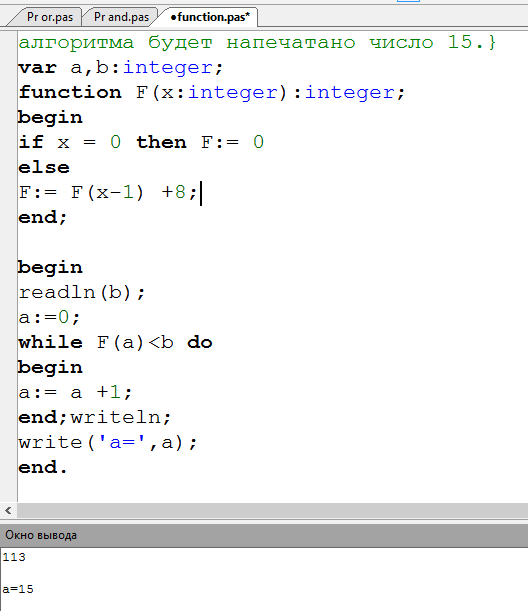
allangarsk:
Программа из задания и результат 15 при в = 113
Автор ответа:
1
Рекурсивная функция f вычисляет значение 8*а.
В самом деле, f(0)=0, f(1)=8; f(2)=16 и т.д.
В основной программе цикл выполняется до тех пор, пока f(a)<b, или иначе, цикл завершится при условии f(a)≥b.
![F(14)\ \textless \ b\leqslant F(15) \\ 8\cdot 14\ \textless \
b\leqslant 8\cdot 15 \\ 112\ \textless \ b\leqslant 120 \to b \in
(112;120], b \in \mathbb N F(14)\ \textless \ b\leqslant F(15) \\ 8\cdot 14\ \textless \
b\leqslant 8\cdot 15 \\ 112\ \textless \ b\leqslant 120 \to b \in
(112;120], b \in \mathbb N](https://tex.z-dn.net/?f=F%2814%29%5C+%5Ctextless+%5C+b%5Cleqslant+F%2815%29+%5C%5C+8%5Ccdot+14%5C+%5Ctextless+%5C+%0Ab%5Cleqslant+8%5Ccdot+15+%5C%5C+112%5C+%5Ctextless+%5C+b%5Cleqslant+120+%5Cto+b+%5Cin+%0A%28112%3B120%5D%2C+b+%5Cin+%5Cmathbb+N)
Переходя к "простому языку получаем, что b должно быть целым числом, находящемся в интервале от 113 до 120. Минимальное значение b в этом случае равно 113.
Ответ: 113
В самом деле, f(0)=0, f(1)=8; f(2)=16 и т.д.
В основной программе цикл выполняется до тех пор, пока f(a)<b, или иначе, цикл завершится при условии f(a)≥b.
Переходя к "простому языку получаем, что b должно быть целым числом, находящемся в интервале от 113 до 120. Минимальное значение b в этом случае равно 113.
Ответ: 113
что-то в Ваших расчетах не так. Эти значения не влияют на условие. Свои расчеты проверил программой. при 112 - печатает 14 а при 113 печатает 15. Может нужно уточнить расчеты?
Скорее, Вам программу надо свою проверить.
Программа из задания и результат 15 при в = 113
Согласен, неправ, 120 - это верхнее значение b, при котором получается a=15. Нижняя граница b - это a(14)+1. Будем исправлять...
Похожие вопросы
Предмет: Русский язык,
автор: erro14
Предмет: Русский язык,
автор: LikaWolf
Предмет: Русский язык,
автор: AnyaLisenkova
Предмет: Алгебра,
автор: elenaevstratenko4746
Предмет: Физика,
автор: Vladyslavaaa