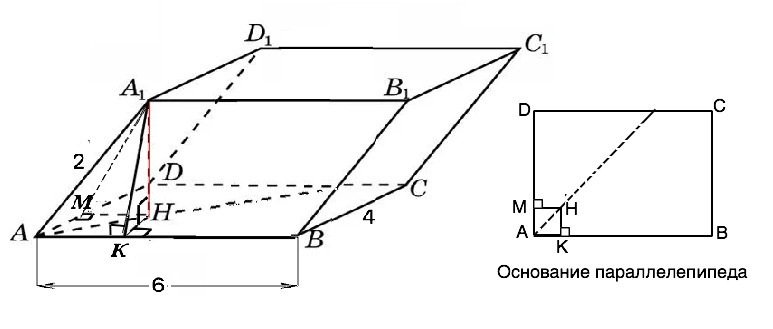
Предмет: Геометрия, автор: viktor479

Основою похилого паралелепіпеда є прямокутник зі сторонами 4 см і 6 см. Бічне ребро
дорівнює 2 см й утворює із суміжними сторонами основи кути в 60°. Знайти об’єм па-
ралелепіпеда.

Ответы

Автор ответа: Hrisula

Основанием наклонного параллелепипеда является прямоугольник со сторонами 4 см и 6 см. Боковое ребро равно 2 см и образует со смежными сторонами основания углы в 60°. Найти объем параллелепипеда.

* * *

Объем параллелепипеда равен произведению площади его основания на высоту. V=S*h

Т.к. основание - прямоугольник, его площадь равна произведению сторон. S=4*6=24 см² Высоту параллелепипеда нужно найти.

Сделаем рисунок. Ребро АА₁ образует со смежными сторонами основания углы А₁АМ и А1АК в 60° .⇒ высоты смежных боковых граней равны. А₁М=А₁К=АА1•sin60=√3 см. АК=АМ=АА1•cos60°=2•1/2=1 см.

Высоты боковых граней – наклонные к плоскости основания, и, так как они равны, равны и их проекции на АВСD. По т. о 3-х перпендикулярах НМ⊥АD, НК⊥АВ. МН=КН=АМ=АК=1. АМНК - квадрат. Перпендикуляр А1Н к основанию АВСD – высота параллелепипеда Из ∆ А1НК по т. Пифагора А1Н=√(A1K²-HK²)=√(3-1)=√2 Объем параллелепипеда V=S•H=24•√2=24√2 ед. объема.

Приложения:

Предыдущий вопрос

Следующий вопрос

Похожие вопросы

Предмет: Другие предметы, автор: Djeka11

Структуры системы образования в Российской Федерации

2 года назад

Предмет: Русский язык, автор: vladloshakov653

Задания по пунктуации. Подготовка к ЕГЭ.
1.Объясните постановку двоеточия в предложении:
1)Как сейчас всё это снова вижу и чувствую кожей: с утра накрапывает, туман залез на забор, все дорожки в лужах.
1) обобщающее слово стоит перед однородными членами предложения;
2) вторая часть бессоюзного сложного предложения поясняет первую;
3) вторая часть бессоюзного сложного предложения указывает на причину;
4) вторая часть бессоюзного сложного предложения указывает на следствие.
2.В каком варианте ответа правильно указаны все цифры, на месте которых в предложении должны стоять запятые?
1.Так хорошо было лежать и писать всякую чушь в дневнике1)прислушиваясь к шороху дождя по крыше2) и 3)зудению комаров на веранде.
1)1 2) 1,2 3) 1,2,3 4) 1,3
2.Ты лежишь на диване 1) закинув забинтованную ногу на спинку2) и читаешь3) какой-то толстый том.
1) 1,3 2) 1,2 3) 2,3 4) 1
3.Укажите правильное объяснение постановки запятой или её отсутствия в предложениях:
1.А мама плавала подолгу ( ) и я каждый раз начинала переживать за неё.
2.Мы скачем по остаткам нашего замка( ) и опять счастливо хохочем.
3.Глаза сузились, мечут молнии ( ) и ещё верхняя губа дёргается , обнажая острые зубки.
1) Простое предложение с однородными членами, перед союзом И запятая не нужна.
2) Сложносочинённое предложение, перед союзом И запятая не нужна.
3) Простое предложение с однородными членами, перед союзом И нужна запятая.
4) Сложносочинённое предложение, перед союзом И нужна запятая.
4.В каком варианте ответа правильно указаны все цифры, на месте которых в предложении должны стоять запятые?
И самое удивительное 1) что эти рифмы уже всегда были2) их нельзя придумать 3) как невозможно придумать самого простого комара 4) или облако из класса долголетающих.
1,2 2) 1,3,4 3) 1,2,3 4) 1,2,3,4
5.В каком предложении необходимо поставить только одну запятую?
1) Он знал все танцы на свете и учил меня танцевать.
2)Волны подкрадываются искоса и испуганные мушки то и дело взлетают.
3)Папа нажимает на педаль уводит ручку управления то вправо то влево.
4)Выходила на балкон и дирижировала нашим двором и соседними домами и деревьями и лужами и облаками.

6.В каком варианте ответа правильно указаны все цифры, на месте которых в предложениях должны стоять запятые?
Осталось в памяти, как мы были у фотографа. Очевидно 1) из-за разочарования, что из ящика не вылетела обещанная птичка. Сделанные тогда фотографии с отцом куда-то исчезли 2) наверное 3) мама уничтожила их.
1) 1, 2, 3 2) 1, 2 3)2, 3 4) 1, 3