Предмет: Математика,
автор: Ludmila12001
Помогите, СРОЧНО!!!!!!
Приложения:
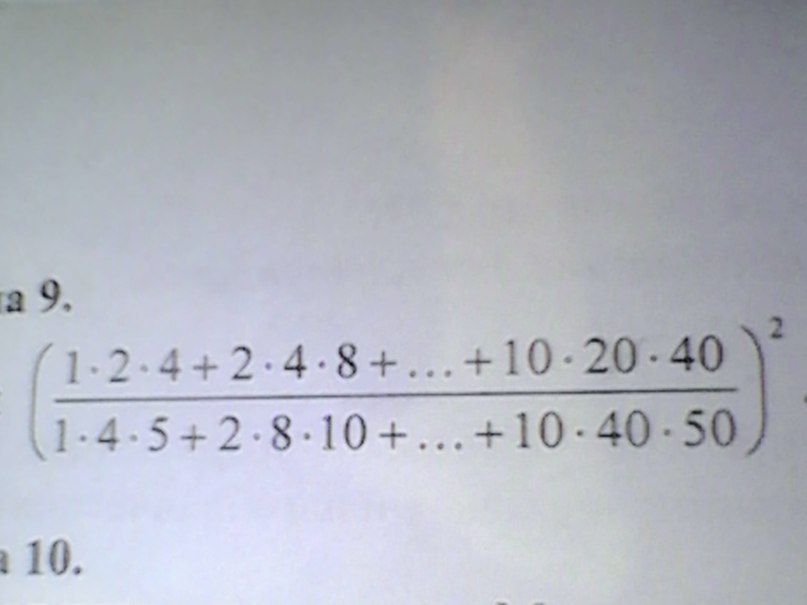
Ответы
Автор ответа:
0
Здесь в числителе и знаменателе дроби - суммы 10 членов геометрических прогрессий вида: bn=b₁·n³,
1) Для числителя (1): b₁,₁ = 1·2·4; q=n³; сумма 10 членов:
Σ=b₁,₁·(1-n³^n)/(1-n³)
2) Для знаменателя дроби(2): b₁,₂ =1·4·5; q =n³;
Σ=b₁,₂·(1-n³^n)/(1-n³)
3) Сравнивая числитель и знаменатель дроби, очевидно, что сомножитель (1-n³^n)/(1-n³) является общим. Значит, его можно сократить.
И наше выражение примет вид:
(1·2·4+2·4·8+...+10·20·40)² /(1·4·5+2·8·10+...+10·40·50)² = (1·2·4)²/(1·4·5)² = 2²/5² =4/25=0,16
1) Для числителя (1): b₁,₁ = 1·2·4; q=n³; сумма 10 членов:
Σ=b₁,₁·(1-n³^n)/(1-n³)
2) Для знаменателя дроби(2): b₁,₂ =1·4·5; q =n³;
Σ=b₁,₂·(1-n³^n)/(1-n³)
3) Сравнивая числитель и знаменатель дроби, очевидно, что сомножитель (1-n³^n)/(1-n³) является общим. Значит, его можно сократить.
И наше выражение примет вид:
(1·2·4+2·4·8+...+10·20·40)² /(1·4·5+2·8·10+...+10·40·50)² = (1·2·4)²/(1·4·5)² = 2²/5² =4/25=0,16
Похожие вопросы
Предмет: Английский язык,
автор: Яна3911
Предмет: Русский язык,
автор: MaryLiveee
Предмет: Русский язык,
автор: posajentaz
Предмет: Алгебра,
автор: София752