Предмет: Математика,
автор: Skolnik1337
Укажите количество корней уравнения √3сos(π/2+x)=2sin(π-x)sin(x+π) . С решением
LFP:
а промежуток указан?? это периодические функции ---решений может быть бесконечно много)))
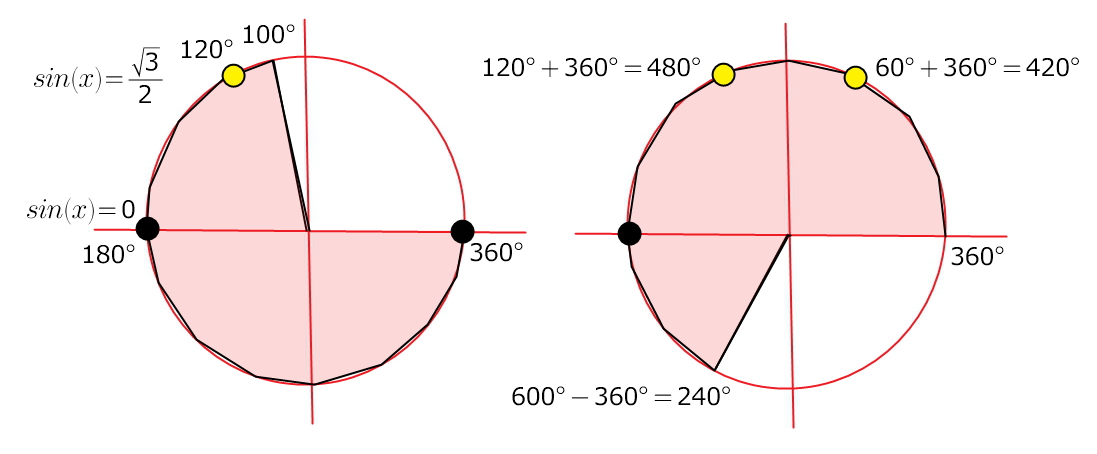
Пардон (100°-600°)
100 тире 600
Ответы
Автор ответа:
2
sin(π-x) = sin(x)
sin(π+x) = -sin(x)
cos(π/2+x) = -sin(x)
-√3sin(x) + 2(sin(x))² = 0
sin(x)*(2sin(x) - √3) = 0
sin(x) = 0 sin(x) = √3/2
100° ---угол во второй четверти
600° ---угол в третьей четверти (через период)))
для первого уравнения в этом промежутке ТРИ корня (черные точки на рис.)
для второго уравнения тоже ТРИ (желтые точки на рис.)
Ответ: шесть корней
sin(π+x) = -sin(x)
cos(π/2+x) = -sin(x)
-√3sin(x) + 2(sin(x))² = 0
sin(x)*(2sin(x) - √3) = 0
sin(x) = 0 sin(x) = √3/2
100° ---угол во второй четверти
600° ---угол в третьей четверти (через период)))
для первого уравнения в этом промежутке ТРИ корня (черные точки на рис.)
для второго уравнения тоже ТРИ (желтые точки на рис.)
Ответ: шесть корней
Приложения:
Спасибо большое
на здоровье!!
Похожие вопросы
Предмет: Английский язык,
автор: ЯTOXA
Предмет: Русский язык,
автор: сара333
Предмет: Английский язык,
автор: boyswow
Предмет: Алгебра,
автор: extedy