Предмет: Математика,
автор: Aluex
решите неравенство решите неравенство
Приложения:
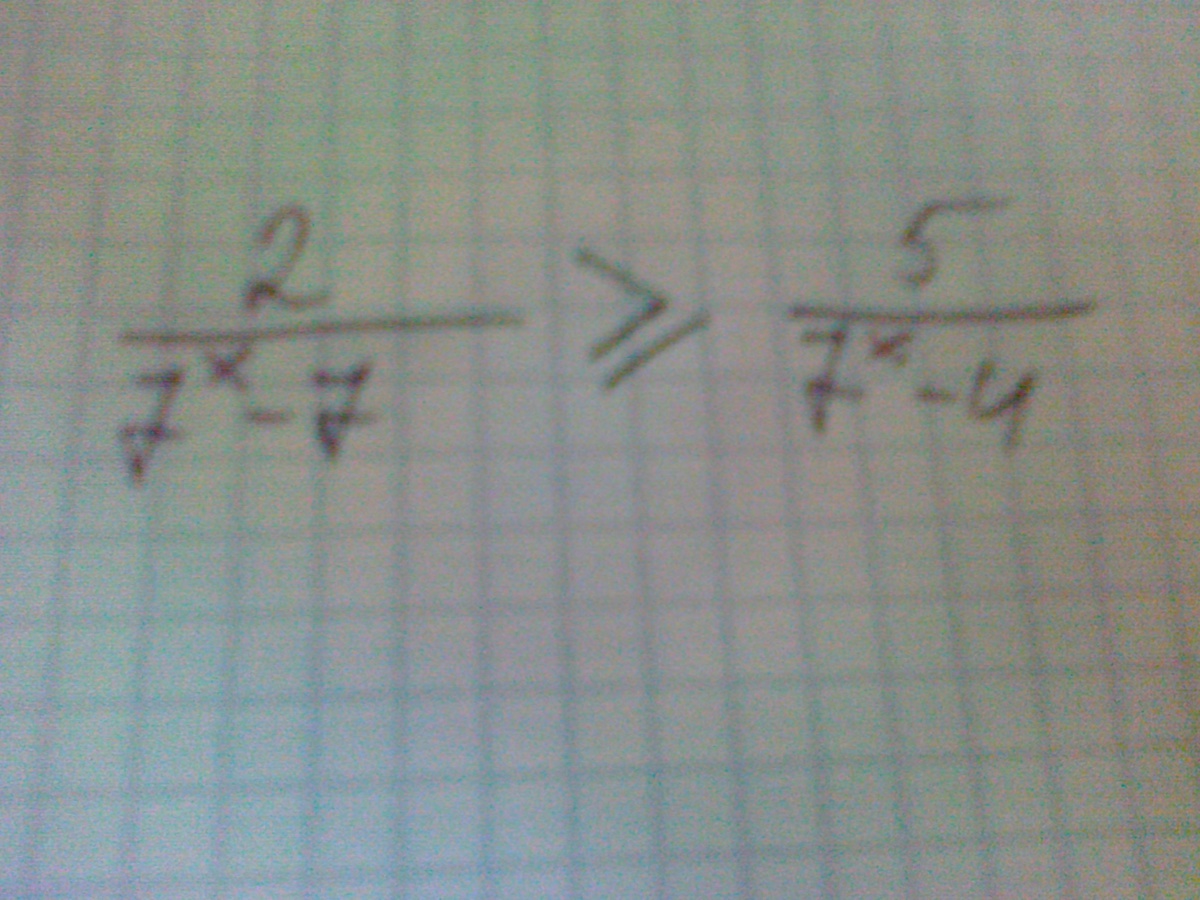
Ответы
Автор ответа:
4
ОДЗ 7^x-7≠0 и 7^x-4≠0
x≠1 x≠log7 4
7^x-7/2≤7^x-4/5
5*7^x-35≤2*7^x-8
3*7^x≤27
7^x≤9
x≤log7 9
c учетом ОДЗ получаем ответ
(-∞;log7 4)∨(log7 4;1)∨(1;log7 9]
x≠1 x≠log7 4
7^x-7/2≤7^x-4/5
5*7^x-35≤2*7^x-8
3*7^x≤27
7^x≤9
x≤log7 9
c учетом ОДЗ получаем ответ
(-∞;log7 4)∨(log7 4;1)∨(1;log7 9]
oganesbagoyan:
(7^x-7)/2≤(7^x-4)/5 ? 2 > -8 ⇒ ? 1/2 < 1/(-8)
2/(7^x -7) ≥ 5/(7^x -4) не ⇔ (7^x -7)/2 ≤ (7^x -4)/5 исправьте
Автор ответа:
1
2/(7^x -7) ≥ 5/(7^x -4) ; * * * обозначим t =7^x >0 * * *
5/(t-4) -2/(t -7) ≤ 0 ;
3(t -9)/(t-4)(t-7) ≤ 0 ;
- + - +
--------- (4 ) ---------(7) ---------- [9] ---------
t ∈(- ∞; 4) U (7 ; 9] , учитывая t =7^x >0 пишем :
t ∈(0; 4) U (7 ; 9] ;
[ 0<7^x <4 ; 7 < 7^x ≤ 9.⇔x ∈( -∞; Loq_7 4) U (1 ;Loq_7 9 ] .
ответ : x ∈( -∞; Loq_7 4) U (1 ;Loq_7 9 ] .
5/(t-4) -2/(t -7) ≤ 0 ;
3(t -9)/(t-4)(t-7) ≤ 0 ;
- + - +
--------- (4 ) ---------(7) ---------- [9] ---------
t ∈(- ∞; 4) U (7 ; 9] , учитывая t =7^x >0 пишем :
t ∈(0; 4) U (7 ; 9] ;
[ 0<7^x <4 ; 7 < 7^x ≤ 9.⇔x ∈( -∞; Loq_7 4) U (1 ;Loq_7 9 ] .
ответ : x ∈( -∞; Loq_7 4) U (1 ;Loq_7 9 ] .
Похожие вопросы
Предмет: Русский язык,
автор: irinaladugina
Предмет: Английский язык,
автор: yashkovaangeli
Предмет: Английский язык,
автор: 12a12aa
Предмет: Биология,
автор: 01247
Предмет: Математика,
автор: Аноним