Помогите найти, пожалуйста. См. приложенный файл
Ответы
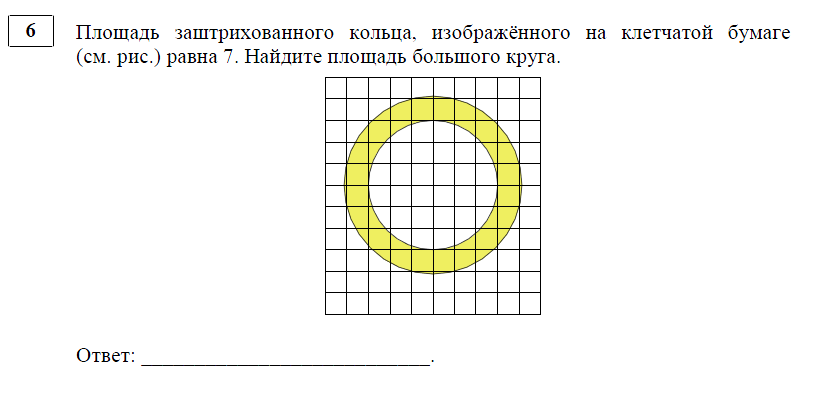
Площадь заштрихованного кольца, изображенного на клетчатой бумаге (см.рис.) равна 7. Найдите площадь большого круга.
----------
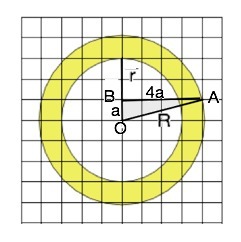
Обозначим радиус малого круга r, большого - R.
Примем длину стороны клетки равной а.
По рисунку легко определить, что r=3а.
Длину R необходимо вычислить, т.к. по клеткам на его вертикальной и горизонтальной оси нет целочисленных пересечений с границей верхнего круга. Но на внешней окружности есть такая точка. Обозначим её А. Точку пересечения отрезка, проведенного параллельно горизонтальному диаметру большего круга, с вертикальным радиусом меньшей окружности – В, центр окружностей – О.
АВ=4а, ОВ=а
Из прямоугольного ∆ АОВ по т.Пифагора
R²=OB²+OA²=a²+16a²=17a²
Площадь кольца равна разности площадей большого и малого кругов.
πR²-πr²=7
π17a²-9πa²=7
8πa²=7⇒
πа²=7/8
π17a²=17•7/8=119/8 (ед. площади)=14,875 (можно округлить до 15)
---------
При решении задач по рисунку с кругом на клетчатом фоне нужно помнить, что нередко радиус нужно вычислить.