Предмет: Алгебра,
автор: BukBear
Найдите наименьшее значение функции на отрезке
Приложения:
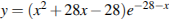
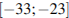
Ответы
Автор ответа:
3
В данный промежуток
Теперь подставим известные точки промежутка в исходную функцию.
Ответ:
Похожие вопросы
Предмет: Английский язык,
автор: kate67676767
Предмет: Английский язык,
автор: козлиб
Предмет: Английский язык,
автор: оксана759ор
Предмет: Русский язык,
автор: hot9796