Предмет: Алгебра,
автор: JJJJJJ28
Какую мат.часть надо повторить, чтобы уверенно решать такое.
Приложения:
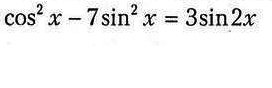
LFP:
решение тригонометрических уравнений... можно начать с определения синуса и косинуса...
это уравнение сводится к квадратному относительно тангенса...
ссылочкой на теорию поделишься ?
учебник... интернет...
здесь нельзя ссылки указывать...
а в лс ?
Ответы
Автор ответа:
0
cos²x-7sin²x-6sinxcosx=0
однородное уравнение второй степени (каждое слагаемое имеет степень 2)
уравнения такого типа решаются методом деления на квадрат одной из переменных (на sin²x или на cos²x) и приводится к квадратному относительно тангенса или котангенса
поделим на cos²x≠0, получим
1-7sin²x/cos²x-6sinxcosx/cos²x=0
1-7(sinx/cosx)²-6sinx/cosx=0
1-7tg²x-6tgx=0
-7tg²x-6tgx+1=0
7tg²x+6tgx-1=0
tgx=-1 tgx=1/7
x=-pi/4+pi*n x=arctg1/7+pi*n
есть тригонометрические однородные уравнения первой степени
asinx+bcosx=0 решается методом делением на sinx или cosx и стодится к тангенсу или котангенсу
уравнения типа
asinx+bcosx=c, где с≠0 решается способом деления на √(a²+b²) и сворачивается по формуле синуса или косинуса суммы (разности)
однородное уравнение второй степени (каждое слагаемое имеет степень 2)
уравнения такого типа решаются методом деления на квадрат одной из переменных (на sin²x или на cos²x) и приводится к квадратному относительно тангенса или котангенса
поделим на cos²x≠0, получим
1-7sin²x/cos²x-6sinxcosx/cos²x=0
1-7(sinx/cosx)²-6sinx/cosx=0
1-7tg²x-6tgx=0
-7tg²x-6tgx+1=0
7tg²x+6tgx-1=0
tgx=-1 tgx=1/7
x=-pi/4+pi*n x=arctg1/7+pi*n
есть тригонометрические однородные уравнения первой степени
asinx+bcosx=0 решается методом делением на sinx или cosx и стодится к тангенсу или котангенсу
уравнения типа
asinx+bcosx=c, где с≠0 решается способом деления на √(a²+b²) и сворачивается по формуле синуса или косинуса суммы (разности)
Похожие вопросы
Предмет: Русский язык,
автор: оля2066
Предмет: Қазақ тiлi,
автор: Nikosto
Предмет: Окружающий мир,
автор: хх2илья2хх
Предмет: Английский язык,
автор: qwertyui7834
Предмет: Физика,
автор: nastya251005