Предмет: Математика,
автор: Хомячонок
Помогите, пожааалуйста
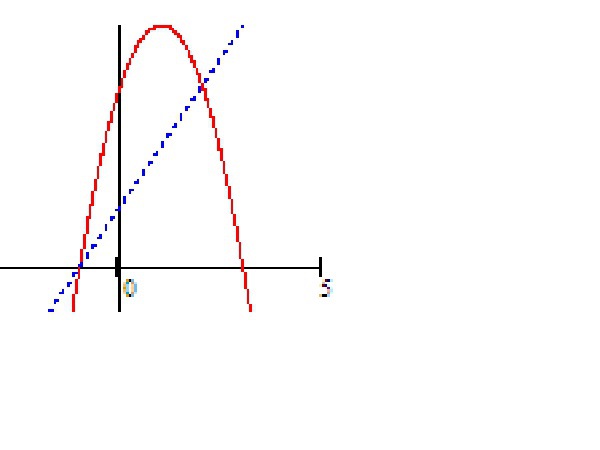
Вычислить площадь фигуры, ограниченной линиями y = 3 + 2x − x^2 ,
y = x +1, y = 0. Сделать чертеж.
Ответы
Автор ответа:
1
в полученное выражение вместо х подставляем 2
в это же выражение подставляем вместо х=-1
затем из первого числа вычитаем второе т.е.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: karslievn
Предмет: Русский язык,
автор: Аноним
Предмет: Английский язык,
автор: svetavip94
Предмет: Русский язык,
автор: alfabulmen