Предмет: Геометрия,
автор: volk9999
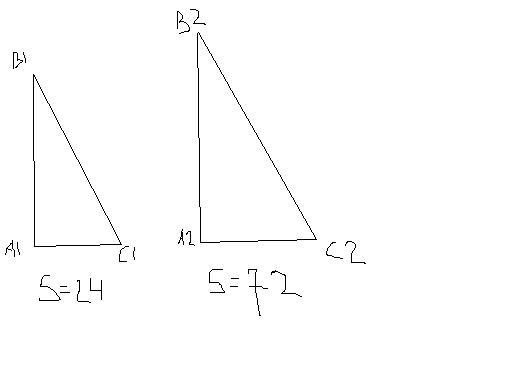
гипотенуза и катет прямоугольного треугольника соответственно равны 10 см и 6 см. Найти наибольшую сторону подобного ему треугольника площадь которого равна 72см²
Ответы
Автор ответа:
1
Катет первого прямоугольного треугольника равен Х=√(10²-6²)=8.
Площадь первого треугольника равна половине произведения катетов, т.е
S=1/2*(6*8)=24
Площадь первого треугольника относится к площади подобного как 1:3, т.к
S1/S2=72/24=3.
Отношение площадей подобных треугольников равно квадрату коэффициента подобия, т.е. катеты относятся:
3=(А2В2/А1В1)² 3=(А2В2/6)² А2В2=6√3 ---катет
3= (А2С2/А1С1)² 3=(А2С2/8)² А2С2=8√3 -----катет
гипотенузы относятся:
3=(В2С2/В1С1)² 3=(В2С2/10)² B2C2=10√3 -------гипотенуза
Проверяем найдём площадь второго треугольника:
S2=1/2*(6√3*8√3)=72
Наибольшая сторона равна 10√3
Площадь первого треугольника равна половине произведения катетов, т.е
S=1/2*(6*8)=24
Площадь первого треугольника относится к площади подобного как 1:3, т.к
S1/S2=72/24=3.
Отношение площадей подобных треугольников равно квадрату коэффициента подобия, т.е. катеты относятся:
3=(А2В2/А1В1)² 3=(А2В2/6)² А2В2=6√3 ---катет
3= (А2С2/А1С1)² 3=(А2С2/8)² А2С2=8√3 -----катет
гипотенузы относятся:
3=(В2С2/В1С1)² 3=(В2С2/10)² B2C2=10√3 -------гипотенуза
Проверяем найдём площадь второго треугольника:
S2=1/2*(6√3*8√3)=72
Наибольшая сторона равна 10√3
Приложения:
spamdriver:
Хорошее решение! Надоело помогать тем кто не ценит помощь!
правда ответ 30 см
но всеодно спасибо
Почему 30? опять.
Надоело свою правоту доказывать! Ответ 10√3 и всё тут.
Удалённое решение чушь полная, нет такой теоремы, чтобы стороны подобных треугольников относились как площади 3 к 1.
Отношение площадей подобных треугольников равно квадрату коэффициента подобия т.е К^2 а отношение сторон равно коэффициенту подобия K. K=√3 (отношение сторон) а K^2=3 (отношение площадей).
Если ваш учитель считает что в ответе 30, то ему на пенсию пора. А уменя 5 лет ФизМата и диплом по Аналитической геометрии на Отлично.
То решение не зря удалили а бессмысленно отвечать, чтобы заработать баллы это ФУУУУУУУУУУ
Похожие вопросы
Предмет: Английский язык,
автор: Englishwoman12
Предмет: Українська мова,
автор: Аноним
Предмет: Другие предметы,
автор: Aru2711
Предмет: Українська мова,
автор: tanjashef
Предмет: Русский язык,
автор: denvisotin2017