Question

Пожалуйста решите
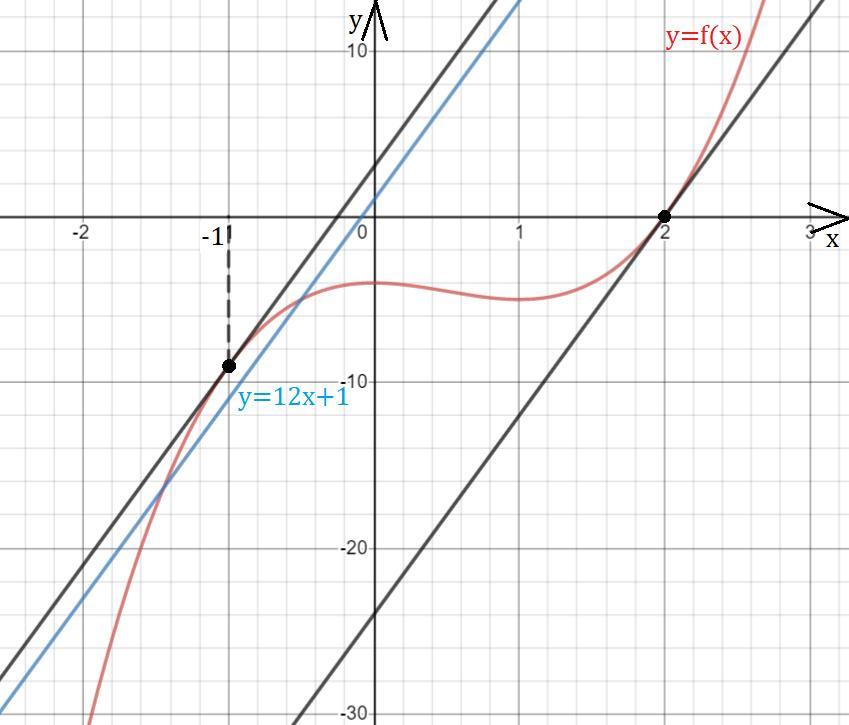
Касательной к графику функции f(x)=2x^3 - 3x^2 - 4 паралельная прямой y=12x+1. Найдите абциссу токи касания. Ответ 2

Answer 1

Тангенс наклона касательной, вида y=kx+b, к графику у=f(x), с абсциссой x₀ у точки касания, равен f'(x₀): tgα=k=f'(x₀).

f(x)=2x³-3x²-4; y=12x+1

Прямые вида y=kx+b параллельны, если k - одинаковый коэффициент. Откуда 12=k=f'(x₀).

f'(x) = (2x³)'-(3x²)'-4' = 6x²-6x

f'(x₀) = $\displaystyle \tt 6x_0^2-6x_0=12$

$\displaystyle \tt x_0(6x_0+6)-2(6x_0+6)=0\\ (6x_0+6)(x_0-2)=0\\ \\\begin{bmatrix}\tt 6x_0+6=0\\\tt x_0-2=0\end{matrix} \quad \begin{bmatrix}\tt x_0=-1\\\tt x_0=2\end{matrix}$

Осталось проверить, что y=12x+1 не является касательной к y=f(x) т.к. эта прямая должна быть параллельна касательной, а не совпадать с ней.

12x+1 = 2x³-3x²-4

2x³-3x²-12x-5 = 0

x²(2x+1) - 2x(2x+1) - 5(2x+1) = 0

(2x+1)(x²-2x-5) = 0

x=-0,5 или x²-2x-5=0, D=(-2)²-4·(-5) = 24 > 0 ⇒ уравнение имеет 3 решения, поэтому y=12x+1 не касается y=f(x). В данном случаи при касании было бы 2 решения.

Ответ: х = {-1;2}.