Предмет: Математика,
автор: конькова
Помогите пожалуйста решить предел
Приложения:
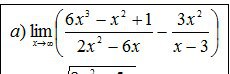
Ответы
Автор ответа:
1
Автор ответа:
1
В пределах с бесконечностью константы(простые числа) можно убирать, т.к. по сравнению с бесконечностью они бесконечно малы, то есть на сам предел не повлияют.
Приложения:

Похожие вопросы
Предмет: Другие предметы,
автор: dimitri23
Предмет: Русский язык,
автор: sapesh
Предмет: Английский язык,
автор: кукушка234234234234
Предмет: Українська мова,
автор: mrrrrliza15
Предмет: Русский язык,
автор: sonya303765