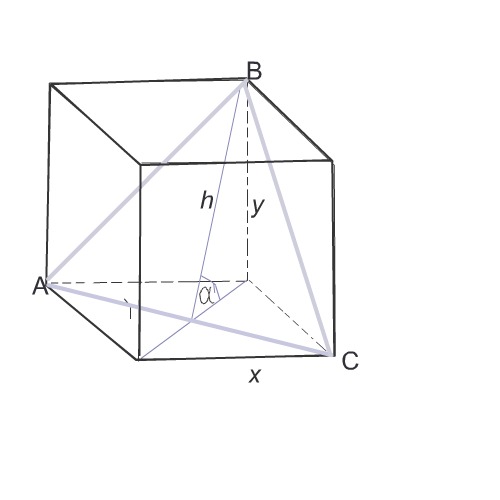
Площадь боковой поверхности правильной четырехугольной призмы равна Q.Сечение призмы,проходящее через диагональ нижнего основания и противолезащую вершину верхнего основания ,образует с плоскостью основания призмы угол фльфа .Найти площадь сечения.
сделайте рисунок и поробное объяснение. решение из интернета а также решение провессора Рензи не переписывайте.
Ответы
Площадь сечения этой призмы - равнобедренный треугольник.
Его боковые стороны АВ и ВС диагонали боковых граней,
основание - диагональ d квадрата, лежащего в основании призмы.
Пусть ребро основания х, боковое ребро у.
Диагональ основания по формуле диагонали квадрата
d=х√2
Высота сечения h
sinα=у:h
h=у:sinα
Sсеч=½·h·d
Sсеч=½·х√2*у:sinα
Sсеч= ½·ху√2:sinα
Площадь одной грани
ху=Q:4
Sсеч=½ ·Q:4 √2 : sinα= ⅛ Q√2:sinα