Предмет: Алгебра,
автор: nastygal55
Помогите решить!!!
(a+1)^3-(a+1)=a(a+1)(a+2)
Приложения:
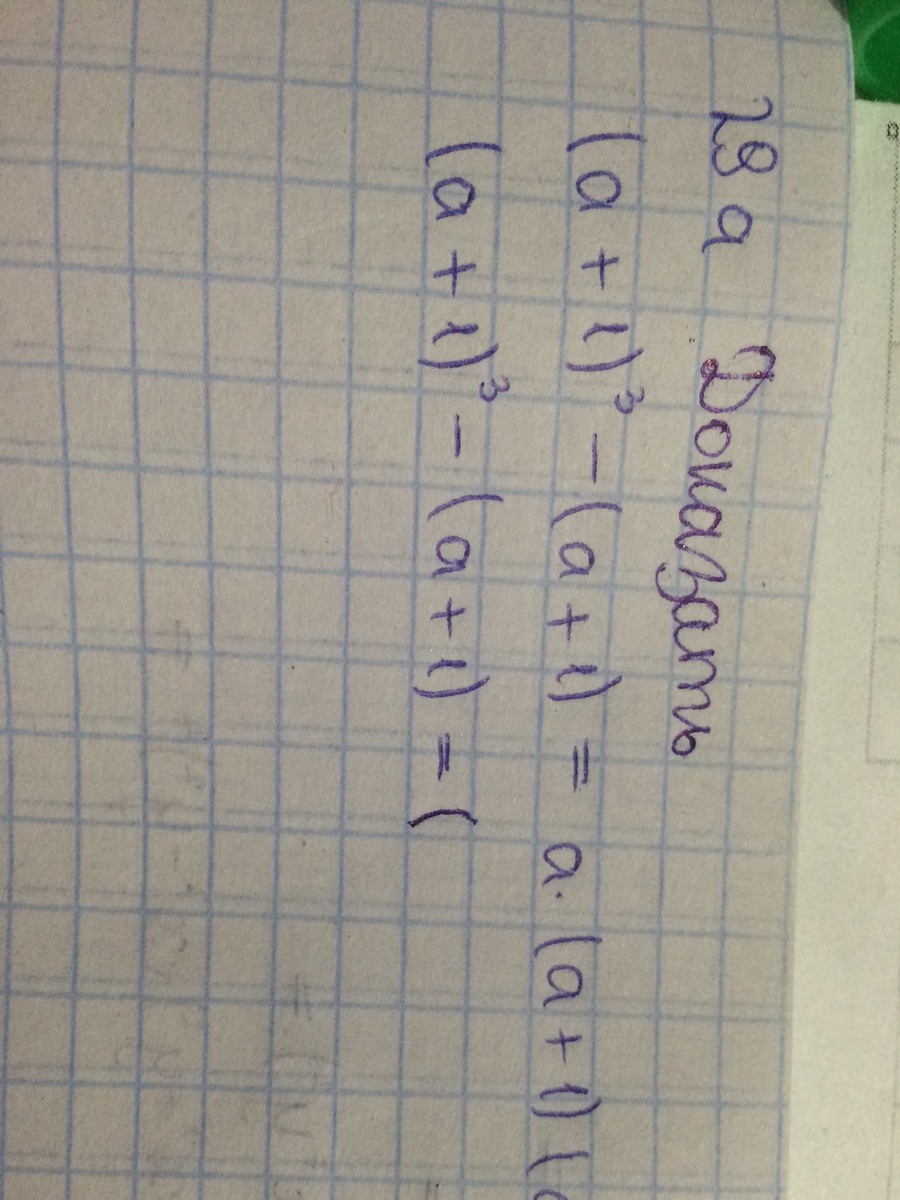
Ответы
Автор ответа:
0
(a+1)^3-(a+1)=a(a+1)(a+2)
(а+1)((а+1)^2-1)-a(a+1)(a+2)=0
(a+1)(a^2+2a+1-1-a(a+2)=0
(a+1)(a^2+2a+1 - a^2-2a)=0
(a+1)=0
a=-1
(а+1)((а+1)^2-1)-a(a+1)(a+2)=0
(a+1)(a^2+2a+1-1-a(a+2)=0
(a+1)(a^2+2a+1 - a^2-2a)=0
(a+1)=0
a=-1
Автор ответа:
0
Как я поняла, тут надо доказать, что правая часть равна левой
доказательство:
a^3 + 3a^2 + 3a + 1 - a - 1 = a(a^2 +2a + a +2)
a^3 + 3a^2 + 2a = a(a^2 + 3a +2)
a^3 + 3a^2 +2a = a^3 + 3a^2 + 2a
доказательство:
a^3 + 3a^2 + 3a + 1 - a - 1 = a(a^2 +2a + a +2)
a^3 + 3a^2 + 2a = a(a^2 + 3a +2)
a^3 + 3a^2 +2a = a^3 + 3a^2 + 2a
Похожие вопросы
Предмет: Английский язык,
автор: Аноним
Предмет: Английский язык,
автор: liiimini
Предмет: Английский язык,
автор: denis2456741
Предмет: Физика,
автор: sahapova7878
Предмет: Математика,
автор: 89901983