Предмет: Геометрия,
автор: ФМТ
Две окружности касаются внешним образом в точке C. Прямая AB касается первой окружности в точки A, а второй - в точке B.
а) Докажите , что прямые AC и BC перпендикулярны друг другу.
б) Найдите площадь треугольника ABC, если радиусы окружностей равны 2 и 8.
terminator13500:
:(
Ответы
Автор ответа:
2
а) треугольники О1АС и СО2В равнобедренные,углы при основании равны
углы АО1С и СО2В односторонние, их сумма = 180
пусть угол АО1С=α, тогда СО2В=180-α
угол О1СА=(180-АО1С)/2=(180-α)/2
O2CB=(180-CO2B)/2=(180-180+α)/2=α/2
ACB=180-O1CA-O2CB=180-(180-α)/2-(α/2)=90
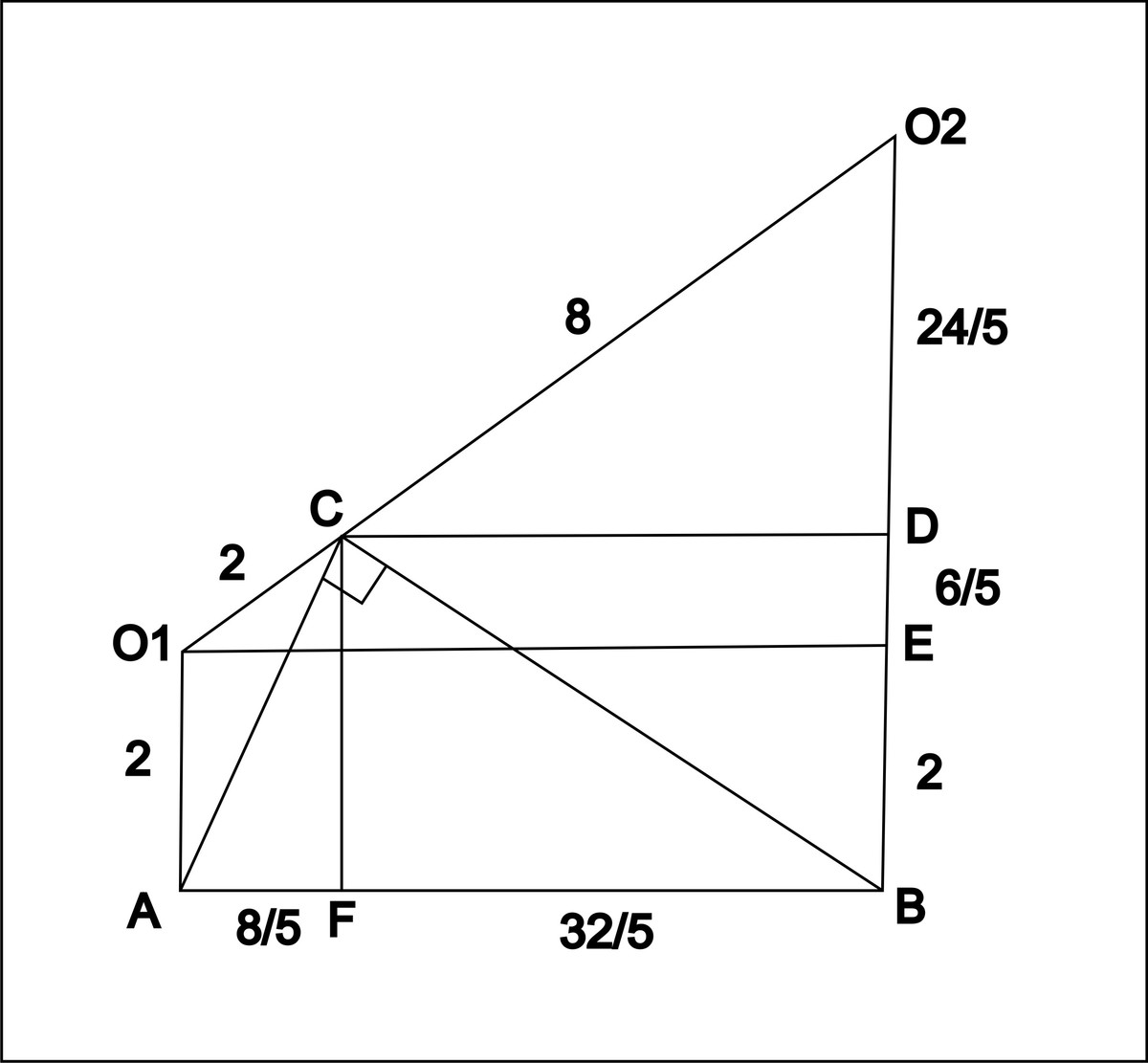
б)по теореме Фалеса
O1C/O1O2=ED/EO2=1/5=ED/6
ED=6/5
O1C/O1O2=AF/AB=1/5=AF/8
AF=8/5
CF=DE+EB=16/5
по теореме Пифагора
AC²=CF²+AF²=(64/25)+(256/25)=320/25
AC=8/√5
CB²=CF²+FB²=(256/25)+(1024/25)=1280/25
CB=16/√5
S(ABC)=AC·CB=128/5=25,6
углы АО1С и СО2В односторонние, их сумма = 180
пусть угол АО1С=α, тогда СО2В=180-α
угол О1СА=(180-АО1С)/2=(180-α)/2
O2CB=(180-CO2B)/2=(180-180+α)/2=α/2
ACB=180-O1CA-O2CB=180-(180-α)/2-(α/2)=90
б)по теореме Фалеса
O1C/O1O2=ED/EO2=1/5=ED/6
ED=6/5
O1C/O1O2=AF/AB=1/5=AF/8
AF=8/5
CF=DE+EB=16/5
по теореме Пифагора
AC²=CF²+AF²=(64/25)+(256/25)=320/25
AC=8/√5
CB²=CF²+FB²=(256/25)+(1024/25)=1280/25
CB=16/√5
S(ABC)=AC·CB=128/5=25,6
Приложения:

Похожие вопросы
Предмет: Русский язык,
автор: vakirill05
Предмет: Окружающий мир,
автор: lazizhamraev040
Предмет: Другие предметы,
автор: shnakinberg
Предмет: Математика,
автор: kirill84286