Предмет: Геометрия,
автор: артур619
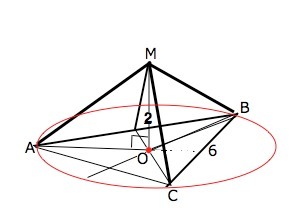
дано треугольник ABC правильный,точка O его центр.прямая OM перпендикулярна к плоскости ABC. 1 1доказать что MA=MB=MC 2.найти MA,если AB=6 см,MO=2 см
Ответы
Автор ответа:
0
МО - перпендикуляр к центру правильного треугольника АВС.
Центр правильного треугольника - точка пересечения высот и является центром описанной вокруг него окружности. Формула радиуса описанной окружности правильного треугольника R=6/√3.
1) ОА=ОВ=ОС=R - равные проекции наклонных МА, МВ, МС. Наклонные с равными проекциями равны. ⇒
МА=МВ=МС
2) Из прямоугольного ∆ МОА по т.Пифагора
АМ=√(AO²+MO²)=√(36/3+4)=√16=4
Приложения:
Похожие вопросы
Предмет: Химия,
автор: kirusha831105
Предмет: География,
автор: ayyniikas
Предмет: Математика,
автор: nazarenok2109
Предмет: Алгебра,
автор: finc2
Предмет: Литература,
автор: Вероника2000