Предмет: Алгебра,
автор: Vinri
Вложение!!!!
Решите уравнение 2cos^3x+корень3сos^2x+2cosx+корень3=0
Указать корни уравнения на отрезке [-2п;-п/2]
Приложения:
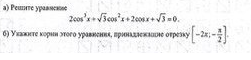
Ответы
Автор ответа:
18
2cosx(cos²x+1)+√3(cos²x+1)=0
(cos²x+1)(2cosx+√3)=0
cos²x+1=0⇒cos²x=-1 нет решения
2cosx+√3=0⇒cosx=-√3/2⇒x=+-5π/6+2πn
-2π≤-5π/6+2πn≤-π/2
-12≤-5+12n≤-3
-7≤12n≤2
-7/12≤n≤1/6
n=0 x=-5π/6
-2π≤5π/6+2ππn≤-π/2
-12≤5+12n≤-3
-17≤12n≤-8
-17/12≤n≤-2/3
n=-1 x=5π/6-2π=-7π/6
(cos²x+1)(2cosx+√3)=0
cos²x+1=0⇒cos²x=-1 нет решения
2cosx+√3=0⇒cosx=-√3/2⇒x=+-5π/6+2πn
-2π≤-5π/6+2πn≤-π/2
-12≤-5+12n≤-3
-7≤12n≤2
-7/12≤n≤1/6
n=0 x=-5π/6
-2π≤5π/6+2ππn≤-π/2
-12≤5+12n≤-3
-17≤12n≤-8
-17/12≤n≤-2/3
n=-1 x=5π/6-2π=-7π/6
Автор ответа:
21
2*cosx*(cos²x + 1) + √3*(cos²x + 1) = 0
(cos²x + 1)*(2*cosx + √3) = 0
1) cos²x + 1 = 0
cos²x = -1
нет решений
2) 2*cosx + √3 = 0
cosx = -√3/2
x = +- 5 π/6 + 2πk
-2π ≤ -5π/6 + 2πk ≤ -π/2
-12 ≤- 5+12k ≤-3
-7 ≤ 12k ≤ 2
-7/12 ≤ k ≤ 1/6
k=0 x=-5π/6
-2π ≤ 5π/6 + 2πk ≤ -π/2
-12 ≤ 5 +12k ≤ -3
-17 ≤ 12k ≤ -8
-17/12 ≤ k ≤ -2/3
k=-1 x=5π/6-2π=-7π/6
(cos²x + 1)*(2*cosx + √3) = 0
1) cos²x + 1 = 0
cos²x = -1
нет решений
2) 2*cosx + √3 = 0
cosx = -√3/2
x = +- 5 π/6 + 2πk
-2π ≤ -5π/6 + 2πk ≤ -π/2
-12 ≤- 5+12k ≤-3
-7 ≤ 12k ≤ 2
-7/12 ≤ k ≤ 1/6
k=0 x=-5π/6
-2π ≤ 5π/6 + 2πk ≤ -π/2
-12 ≤ 5 +12k ≤ -3
-17 ≤ 12k ≤ -8
-17/12 ≤ k ≤ -2/3
k=-1 x=5π/6-2π=-7π/6
Похожие вопросы
Предмет: Русский язык,
автор: nickiforova020117
Предмет: Қазақ тiлi,
автор: Диасномер1
Предмет: Другие предметы,
автор: Ilshatopka
Предмет: Английский язык,
автор: xoooooooxgh
Предмет: Математика,
автор: qwertyu660